全部分类/
教育教学/
中学数学·高中版

中学数学·高中版

2025年03期

扫码免费借阅

目录

快速导航

特色展台 | 逻辑星辉映思维，推理探究启新知

特色展台 | 逻辑星辉映思维，推理探究启新知

摘要：2024年全国新高考Ⅰ卷第19题是新定义题，对学生思维能力的考查提出了更高的要求.本文中从归纳、递推等多角度分析和解决问题，并进行试题变式和溯源，形成解决一类问题的系统性方法.为了突破此类问题，教师在教学中应该重视知识的生成与应用，搭建思维平台，聚焦逻辑推理能力和探究能力，发展核心素养，推进真正的素质教育. 关键词：新定义；思维；逻辑推理；教学新高考背景下，全国卷试题结构不断创新，尤其
特色展台 | 二面角的概念与二面角的平面角教学

特色展台 | 二面角的概念与二面角的平面角教学

本节课选自上海教育出版社《普通高中教科书数学必修第三册》第10章第4节“平面与平面的位置关系”的第2课时——“二面角”，该课时内容分为二面角的平面角、平面与平面垂直两部分，本节课只学习二面角的平面角. 二面角是刻画两个相交平面位置关系的概念和一种度量方式，虽然新课程标准并未对二面角的概念提出明确要求，但其教学一方面是为了知识体系的完整性，另一方面也为学生进一步发展空间想象能力与逻辑推理能力提供了
特色展台 | 情境丰富问题驱动教书育人

特色展台 | 情境丰富问题驱动教书育人

对邓佳敏的“二面角的概念与二面角的平面角”这节课总体感觉是“情境丰富，问题驱动，教书育人”.无论是问题引入、二面角定义的合理性阐述、还是最后的活动3、活动4（例题），都提供了大量生动的学习情境，老师以问题串的形式开展教学，由于问题适合学生实际水平，教学效果好. 还有一个既贯穿课堂始终又“不显山露水”教学活动就是将育人融入其中.下面谈些具体体会. 1 学生活动充分本课自始至终学生参与的机会多
课程视点 | 如何把教科书中的数学问题转变为建模问题

课程视点 | 如何把教科书中的数学问题转变为建模问题

摘要：课程标准要求切实将数学建模融入日常教学中，要做到这一点，至少需要在日常教学中能遇到建模问题.但在教材里除某些章节中特意设置的数学建模问题，不管是例题还是习题中建模问题一般并不常见.本文中首先区分了教材中常见的应用题和建模问题的不同，在此基础上例举了如何将教科书中不同知识领域的数学问题逐步转变为建模问题. 关键词：过渡；建模问题；数学问题 2017版高中数学课程标准将“数学建模”作为六大核
课程视点 | 椭圆的一个“小题大做”的优美结论

课程视点 | 椭圆的一个“小题大做”的优美结论

摘要：从“已知椭圆焦点三角形面积求椭圆上点的坐标”这个常见问题和椭圆的一个常见二级结论出发，历尽发问、探索与再探索以及不懈思考，最终得到“椭圆焦点三角形中椭圆上的点P的坐标与顶角θ之间关系”的简洁优美的数学表达式.探索过程中，好奇心与求知欲是探索点P的纵坐标与角θ之间关系的最初动机；见多识广与名师指引是继续探索二者关系的动力；终身学习与不懈思考是最终得到二者关系的保障.在整个过程中，体验了数学探索
课程视点 | 层层剖析，激发学生的创造力

课程视点 | 层层剖析，激发学生的创造力

摘要：教材习题不仅是检测学生对所学知识掌握情况的优秀素材，而且还是教师引导学生对所学知识进行整合的好帮手.教学中，有目的地选择典型习题，精心设计问题，引导学生对其层层剖析，能有效激发学生的创造力，进一步提升学生分析问题和解决问题的能力. 关键词：教材；习题；问题设计；创造力常言道：“温故而知新.” 常言道，温故而知新.要帮助学生巩固所学的知识，教师就要根据教学进度，有目的地选择教材中的典型
课程视点 | 融入数学文化，探究体积应用

课程视点 | 融入数学文化，探究体积应用

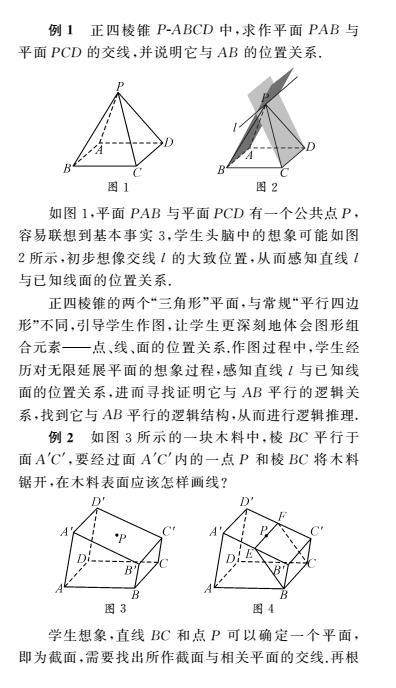
数学文化是数学知识形成与进化的一个基本历程，在数学知识学习与应用过程中自然而然加以渗透与应用.特别是在高中数学教材中，以教材知识、课后阅读教材、提升拓展知识等形式来展示，借助教材中的相关栏目，如“探究与发现”“阅读与思考”“文献阅读与数学写作”等来合理介绍与引导学生阅读与理解.而巧妙挖掘与综合应用相应的数学文化知识，对于提升学生的文化内涵、数学综合应用能力及创新思维等都有很好的帮助，因此，在应用新
教法探索 | 关于平面无限延展性的教学思考

教法探索 | 关于平面无限延展性的教学思考

摘要：平面作为几何公理体系中的一个基本概念是不加以定义的，高中数学立体几何初步的教学是借助几个基本事实，通过直线的无限延伸性来刻画平面的无限延展性的.加强学生对平面无限延展性的理解，加深学生对空间无限性的感悟，对学生空间想象能力的提高、空间观念的形成等有着极其重要的意义.本文中提供三种教学设计方法，引导学生逐步建立平面无限延展性的空间观念，培养学生直观想象、逻辑推理等数学核心素养. 关键词：平面
教法探索 | 注重类比思维，聚焦核心素养

教法探索 | 注重类比思维，聚焦核心素养

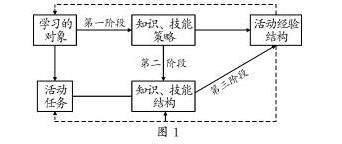
摘要：以“椭圆及其标准方程”的教学为例，类比圆的学习帮助学生理解椭圆的定义及标准方程的推导，引导学生建立新旧知识之间的联系，构建数学知识框架，充分发挥学生学习的主体地位，注重教会学生学习，提升学生数学核心素养. 关键词：类比思维；数学核心素养；椭圆类比思维从两个事物之间的相似性特征入手，结合具体的概念、特征来帮助学生认识数学知识[1].在数学中，通常利用类比思维来探索新知识，从已学知识入手，
教法探索 | 素养立意下高中数学学能课程教学模式建构与应用策略研究

教法探索 | 素养立意下高中数学学能课程教学模式建构与应用策略研究

摘要：素养提升背景下，高中数学学能课程被摆在更加重要的位置.文章首先概述相关理论，并提出三种高中数学学能课程教学模式，然后结合教学实践提出三点教学策略. 关键词：高考数学；学能课程；教学模式；应用策略本研究的重点是建构在培养数学学科核心素养基础上指向学生可持续优质成长的校本课程.具体而言，我们将采用创新的教学方法和教学评价，来提升学生学习数学的关键能力，并激发学生学习数学的动能.这类研究有助
教法探索 | “创艺”融合理念下“函数的概念”教学设计

教法探索 | “创艺”融合理念下“函数的概念”教学设计

摘要：核心素养时代的教学是为了发展学生的学科素养，将思维的发展融入到具体的教学活动中，培养学生的创新能力、问题求解能力和批判性思维.根据艺术教育和创新教育的学习特点，需要不断优化学生的学习途径和教师的教学方式.因此，提出课堂教学融合“创艺”，通过日常教学中艺术教育和创造教育的融合，发挥数学的科学、人文、应用和审美价值，促进学生核心素养的发展. 关键词：核心素养；“创艺”融合；函数概念 1 引言
教法探索 | 素养为本的重组单元“承启”课教学研究

教法探索 | 素养为本的重组单元“承启”课教学研究

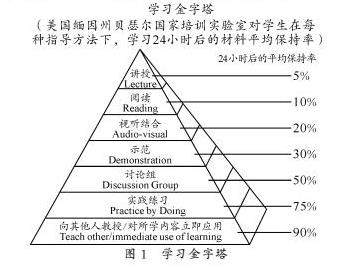
摘要：在核心素养背景下，以“两条直线的位置关系”教学为例，围绕核心问题以逻辑推理为主线设计单元教学的第二课时——承启课教学，探索在课时制的背景下如何行之有效地落实单元教学、发展学生思维.教学过程结合前期知识分析，用多种方法进行演绎推理，最后运用类比思想解决垂直关系的判定. 关键词：承启课；逻辑推理；两条直线的位置关系开展基于核心素养的教学，需要围绕五大主线，把一些具有逻辑联系的知识点放在一起
教法探索 | 借助情景燃点启动思维火花

教法探索 | 借助情景燃点启动思维火花

摘要：本文中探索了情景教学法在高中数学新授课课堂的应用，该方法以创设教学情境为手段，以发展学生数学学科核心素养为导向，以培养学生的探究、思维能力为目标，营造浓厚的学习氛围，让学生积极投入数学学习，感受数学的应用价值和文化价值.结合“等比数列的前n项和”教学实践，阐述了情景教学法在课堂三阶段的应用过程，实践证明该方法激发了学生的学习热情，提升了课堂教学质量，是一种有效的教学方法. 关键词：情景教学
教法探索 | 基于GeoGebra的高中数学可视化教学

教法探索 | 基于GeoGebra的高中数学可视化教学

可视化教学是一种十分有效的教学方法，它能够激发学生学习兴趣、提高教学效率、更好地满足学生的多样化需求.但进行数学的可视化教学时，需要考虑哪些原则？如何在设计高中数学内容的可视化教学时保持合理和科学？运用现代技术进行教学时应该注意哪些问题？在思考上述问题的基础上，以认知负荷理论、数学多元表征学习等理论为支撑，笔者对高中数学可视化教学设计进行了深入思考，以高中数学“椭圆及其几何性质”为例，借助GeoG
学生学习 | 在反省中激活学生的数学直觉思维

学生学习 | 在反省中激活学生的数学直觉思维

摘要：数学直觉思维是指不经过逻辑的、有意识的推断而识别数学对象，并对其进行迅速的判定和直接的领悟.培养可控、合理、有价值的数学直觉思维，有助于提高学生对学习数学的热情.文章从情境创设和问题设计、知识结构、解题操作三方面分析反省，以典题为例，旨在教学过程中引导学生不断地反省，为产生有效的直觉提供源泉. 关键词：直觉思维；反省；数学基本活动经验数学直觉思维是人脑对数学对象进行潜意识的推理，快速判
学生学习 | 数列与其他知识点的交汇融合

学生学习 | 数列与其他知识点的交汇融合

在“知识网络交汇点处设计试题”是高中数学课标的明确要求与高考数学命题的重要指导思想之一.作为高中数学知识中的一大主干知识，数列模块知识是考查数学基础知识与能力综合的一个基本场所，成为高考数学中创新意识与创新应用的一大重要阵地. 1 等差数列与等比数列的交汇借助等差数列与等比数列这两个不同类型的数列之间的交汇，合理“串联”起数列的基本概念、基本公式与基本性质等，成为数列中常见的一类综合应用问题
学生学习 | 嵌套函数的零点问题刍议

学生学习 | 嵌套函数的零点问题刍议

摘要：嵌套函数的零点问题常见于高考和各类模拟试题的压轴小题，是函数中的难点.本文中重点探讨了常见两大嵌套函数考向——“自（互）嵌套型”和“二次嵌套型”的解题思路及方法，其中自（互）嵌套型考向总结出了5种题型，二次嵌套型考向总结了2种题型. 解题的总体思路是先通过“换元”达到“解套”的目的，再利用数形结合、分类讨论等思想具体分析. 目的是让学生能更全面地学习、掌握嵌套函数的零点问题，培养运算、作图、
学生学习 | 谈高三复习中解题思路的建立和形成

学生学习 | 谈高三复习中解题思路的建立和形成

在高三数学复习课堂上，常规过程是教师先引领学生复习知识点，然后进行习题讲解.在这个过程中除“双基”外，还应该关注学生基本思想和基本活动经验的培养，引导学生多进行知识梳理、方法整合和思维提炼，以此提升数学素养.笔者以一节“空间向量的数量积运算”高三复习课教学为例，浅谈如何培养学生的解题思路，进而有效提升学生的解题能力. 1 知识梳理教师呈现问题，学生进行知识梳理. 生1：在正四面体的背景下，
学生学习 | 挖掘特征巧换元，最值求解妙突破

学生学习 | 挖掘特征巧换元，最值求解妙突破

摘要：基于代数式最值（或取值范围）问题的求解，换元法是比较常见的一种技巧、方法.本文中结合题设场景的不同形式，就比较常见的分式问题、积式问题、混式问题及创新问题等典型实例加以剖析与应用，归纳总结换元技巧与对应策略，指导数学教学与解题研究. 关键词：代数式；最值；分式；积式；基本不等式借助换元法思维处理代数式的最值（或取值范围）问题，是基于不等式的基本性质、基本不等式的放缩与应用下的一种基本思
学生学习 | 圆锥曲线中斜率和（积）的定值与定点问题

学生学习 | 圆锥曲线中斜率和（积）的定值与定点问题

摘要：涉及圆锥曲线上的三角形应用问题，是圆锥曲线综合应用问题中的一个重要情境.结合三角形中对应两边的斜率之和（或积）为定值以及第三边的位置特征或斜率值，借助典型实例进行剖析与应用，归纳总结此类应用问题的基本类型与解题技巧，助力数学教学与复习备考. 关键词：圆锥曲线；三角形；直线；斜率；定值；定点直线与圆锥曲线的位置关系的综合应用问题中，经常涉及圆锥曲线上的三角形应用问题，是高考命题中的一个基
学生学习 | 依托复数几何意义，巧妙解决应用问题

学生学习 | 依托复数几何意义，巧妙解决应用问题

摘要：复数的几何意义是复数自身基本知识的延伸与拓展，也是数形结合的一个典型例证.本文中结合复数的几何意义，依托一些常见应用场景与实例，就复数的概念、运算、轨迹问题及创新问题等方面，剖析复数几何意义应用的内涵实质，归纳总结解题规律与技巧，优化解题效益，培养数学核心素养. 关键词：复数；几何意义；概念；运算；轨迹借助平面直角坐标系的建立与复平面的引入，巧妙将代数问题中的复数与几何问题中复平面内的
学生学习 | 三角函数周期确定的“四法”技巧

学生学习 | 三角函数周期确定的“四法”技巧

摘要：作为三角函数的一个基本性质，三角函数周期的确定与应用，是高考命题中比较常见的一个基本知识点与考查点.如何有效、合理、快速、简捷地确定三角函数的周期，为三角函数问题的分析与应用创造条件？本文中结合典型实例，就确定三角函数周期的“四法”加以剖析，助力数学教学与学习. 关键词：三角函数；周期；公式；定义；图象三角函数模块作为高考命题中的基本知识与主干知识之一，其中三角函数的基本性质的考查更是
学生学习 | 立几体积巧求解，分割补形总相宜

学生学习 | 立几体积巧求解，分割补形总相宜

摘要：有关空间多面体中的柱、锥、台及简单组合体的计算问题，大都是通过“分割”与“补形”来进行简化与处理.台补锥、台割锥、柱割锥、锥补柱、利用截面“化斜为直”、“化非规则为规则”等都是常用的方法和技巧.结合实例，就割补法中“割”与“补”的一些常见类型加以剖析，总结规律，指导数学教学与研究. 关键词：立体几何；体积；分割；补形；应用空间立体几何中割补法的运用一般是将复杂、不规则、不易认识的几何体
学生学习 | 立足典型问题，优化复数运算，发散思维应用

学生学习 | 立足典型问题，优化复数运算，发散思维应用

摘要：解决复数及其应用问题时，复数的基本运算是解题中最重要的一个环节，而优化数学运算，提升解题效益成为解题的关键之一.结合一道复数模拟题，合理挖掘对应的技巧与策略，发散数学思维，归纳优化运算思维的技巧与策略，帮助学生全面提升数学能力，优化数学品质，培养数学核心素养. 关键词：复数；性质；方程；待定系数；三角形式复数及其综合应用问题，往往离不开复数的基本运算.而实际进行复数的基本运算时，关键在
评价透视 | 基于高考评价体系的近两年新高考Ⅰ卷数列试题分析

评价透视 | 基于高考评价体系的近两年新高考Ⅰ卷数列试题分析

摘要：高考评价体系为试题分析提供了重要指导.文章梳理了2023和2024年新高考Ⅰ卷中的数列试题，基于高考试题评价体系，从核心价值、学科素养、关键能力、必备知识四个方面对试题进行分析，给出关于数列教学的备考建议. 关键词：高考评价体系；数学试题；备考建议通过梳理发现，在数学新高考Ⅰ卷中，数列试题占据了重要地位，主要体现在其考查内容的广泛性和对学生数学思维能力的综合考查.数列问题不仅涉及基础的
评价透视 | 整体剖析话全局，细节切入详分析

评价透视 | 整体剖析话全局，细节切入详分析

摘要：结合2024年高考数学新高考Ⅱ卷，从整体与细节等多个方面切入，基于高考真题，就新高考试卷的设置情境、教考衔接、深化基础、突出主干、素养考查等方面入手，对比试卷的变化情况、命题风格及命题特色等，从中合理总结点滴命题规律，给出高考复习备考建议，以指导后继的数学教学. 关键词：高考；数学；整体；全局；基础 2024年高考数学新高考Ⅱ卷进一步全面贯彻党的教育方针与二十大精神，有效落实“立德树人”
评价透视 | 基于难度模型的近两年新高考Ⅰ卷解几试题分析及教学启示

评价透视 | 基于难度模型的近两年新高考Ⅰ卷解几试题分析及教学启示

摘要：文章根据五维难度模型，对2023年与2024年新高考Ⅰ卷的解析几何试题从背景材料、知识含量、设问方式、推理水平、认知水平五个方面进行分析，最后给出教学启示. 关键词：数学新高考；难度模型；解析几何试题分析；教学启示 1 五维难度模型我国学者鲍建生参照我国数学课程的特性，确定了以“背景材料、知识含量、设问方式、推理水平、认知水平”为影响因素的数学试题综合难度模型[1]（如图1）. 背
评价透视 | 追踪高考脉络探寻方法本质

评价透视 | 追踪高考脉络探寻方法本质

摘要：本文是一道新概念新定义题目的命制过程.追踪极点极线的历史逻辑和知识关联，从射影几何中的调和点列入手，抓住其知识本质，引导学生学会并且会学，感受数学知识发展逻辑过程，感悟数与形的融通，经历从形到数，又从数到形的过程，旨在考查学生自学能力、数学抽象能力、逻辑推理能力，也考查学生的个性品质. 关键词：试题命制;调和点列;数形融通;个性品质 1 原创试题数学家们早在古希腊时期发现了一组满足特
评价透视 | 自主编题促提高

评价透视 | 自主编题促提高

摘要：在数学教学中对于全概率公式与贝叶斯公式学生往往感觉很抽象，难以掌握.传统的题海战术，加重了学生的负担，对学生的身心健康极为不利，而且也限制了学生的创新意识.本文中以激发学生自主编题为教学案例，通过生活中一些非常鲜活的实例，促使学生切实地感受到数学来源于生活.学生学习变被动为主动，发展数学思维，进而提高课堂效率. 关键词：全概率公式；贝叶斯公式；自主学习；编题长期以来，大部分高中数学教师
评价透视 | 一类高考导数真题的探究及新题命制

评价透视 | 一类高考导数真题的探究及新题命制

摘要：本文中基于2023年新高考Ⅱ卷第22题、2022年新高考Ⅱ卷第22题及2023年甲卷理科第21题，从通法通性的视角探究其解法，得到此类导数题的一般规律，并对此类试题的命制进行分析，命制了两道新试题. 关键词：新高考；导数；高三复习；试题命制 1 试题呈现题1（2023年新高考Ⅱ卷第22题）（1）证明：当0<x<1时，x－x2<sin x<x；（2）已知函数
评价透视 | 基于2022年甲卷圆锥曲线压轴题的原创题命制

评价透视 | 基于2022年甲卷圆锥曲线压轴题的原创题命制

摘要：本文中以2022年甲卷圆锥曲线压轴题为背景，命制了一道抛物线的原创题，并通过对原创题的题源——“坎迪定理”问题进行分析，对其在椭圆中的情形命制了一系列原创题，落实对学生数学核心素养的培养. 关键词：核心素养;坎迪定理;定值;定直线 1 试题呈现与分析原创题1抛物线G：y2=2px（p>0）的焦点为F，过点F的直线l1与G交于A，B两点，过点F的直线l2与G交于C，D两点，当l1
评价透视 | 社会生活情境下的数学抽象素养三种水平试题赏析及命题启示

评价透视 | 社会生活情境下的数学抽象素养三种水平试题赏析及命题启示

摘要：社会生活情境是培养数学抽象素养的重要载体.文章对不同情境下的数学抽象素养三种水平试题进行分析，并得出两点命题启示. 关键词：高中数学；社会生活情境；数学抽象素养；命题启示 1 社会生活中科学技术及智力挑战例1（数学抽象水平一）在一档节目中，一位选手展示了惊人的脑力，他能够准确地记住圆周率π并快速背诵小数点后200位数字.值得注意的是，当评委提到小数点后的任何一位数字（不超过200位时
解题天地 | 巧借三角形全等条件，妙设未知量解三角形

解题天地 | 巧借三角形全等条件，妙设未知量解三角形

摘要：利用正弦定理与余弦定理解平面几何问题是高考的热点，其中需要设未知量的题目是一个难点.本文中巧借初中学的全等三角形的判定条件，先定性分析已知条件需要补充哪些条件可以唯一确定三角形，再妙设需要补充的边或角为未知量，最后根据正弦定理、余弦定理进行定量计算，从而为学生寻找到解平面几何复杂问题的方法. 关键词：全等三角形;全等判定;解三角形;余弦定理；正弦定理解三角形是高考中的热点，一般考查正弦
解题天地 | 数形结合思想巧解题，对数函数图象妙应用

解题天地 | 数形结合思想巧解题，对数函数图象妙应用

摘要：正确理解并掌握对数函数的图象与性质，借助数形结合思想来分析或处理与对数函数的图象和性质相关的问题，成为对数函数模块知识考查的一个重要方向.本文中以对数函数图象为依托，结合典型实例，应用数形结合思想处理一些与之相关的综合应用问题，归纳总结解题技巧与策略. 关键词：对数函数；图象；数形结合；参数；方程对数函数是高中数学中基本的初等函数模型之一，是继幂函数、指数函数后又一重要的函数模型，是中
解题天地 | 依托指数函数图象，数形结合解决问题

解题天地 | 依托指数函数图象，数形结合解决问题

摘要：正确理解并掌握指数函数的图象与性质，借助数形结合思维来分析或处理与指数函数的图象与性质相关的问题，成为指数函数模块知识考查的一个重要方向.以指数函数图象为依托，结合典型实例，利用数形结合处理一些与之相关的综合应用问题，归纳总结解题技巧与策略，指导数学教学与复习备考. 关键词：指数函数；图象；数形结合；参数；代数式指数函数是高中数学中基本的初等函数模型之一，也是重要的函数模型，是中学基本
解题天地 | 2023年全国高考数学I卷第17题13解

解题天地 | 2023年全国高考数学I卷第17题13解

摘要：本文中以2023年全国高考数学I卷第17题为载体，给出解三角形的五种常规解题路径.（1）通解，运用解三角形相关知识求解；（2）特征构造法，抓住条件和所求的特征，构造相应的图形作答；（3）解析几何法，通过建系，利用解析几何相关知识作答；（4）向量法，通过建系，借助向量相关知识作答；（5）几何法，利用初中平面几何相关知识作答.通过分析，促使学生能够结合具体题目，运用五种路径熟练解决一类解三角形问
解题天地 | 巧用思维导图优化解题教学

解题天地 | 巧用思维导图优化解题教学

数学的解题过程就是思维的呈现过程，良好的思维是破解难题的一把利刃，是学生对难题迎刃而解的保障.所以，在解题教学中，教师应思考如何运用教学方法，激发学生的思维，促使学生学会思考，学会解题，从而积累解题活动经验，促进学科素养的形成与发展.教学实践中发现，将思维导图融入解题教学中，可有效建构知识框架，搭建思维体系，大大提高学习效果.文章以2023年高考全国甲卷理科第21题为例，探析思维导图在解题教学中的
解题天地 | 公切线场景设置，巧思维与妙拓展

解题天地 | 公切线场景设置，巧思维与妙拓展

摘要：涉及多曲线（特别是两条曲线）的公切线问题，是高考数学试卷中一类创新应用问题，综合性强，较新颖.结合一道两个含参函数存在过确定点的公切线问题，从不同数学思维切入与应用，呈现一题多解，深入探究与应用，实现一题多变，引领并指导数学教学与复习备考. 关键词：函数；公切线；常规；特殊；极端多曲线（特别是两条曲线）的公切线问题，是近年新课标高考数学试卷中的创新热点问题.此类问题以多条曲线（一般以两
解题天地 | 常规三角变换，特殊思维应用

解题天地 | 常规三角变换，特殊思维应用

摘要：借助三角恒等变换公式来合理考查逻辑推理与数学运算，通常是高考中三角函数模块考查的热点与难点.以一道模拟题中的三角函数值的求解为例，从三角恒等变换公式与特殊值等视角切入，剖析问题的解决技巧与方法，归纳总结解题技巧与策略，引领并指导数学教学与复习备考. 关键词：三角函数；三角恒等变换；特殊值；变式三角函数中的三角恒等变换公式，是涉及一个角或两个角之间的一组特殊恒等公式，是满足条件的角的变化
解题天地 | 高考分段数列试题的解法探究与变式教学

解题天地 | 高考分段数列试题的解法探究与变式教学

摘要：分段数列的求解问题是高考热点，也是难点，本文中以两道高考真题为例谈谈这类问题的解法探究与变式教学. 关键词：分段数列；高考真题；解法探究高考试题是命题专家们深度思考、团队协作后命制出来的，不仅能够考查学生的思维品质和关键能力，而且能够引导中学教学.数列高考题中，分段数列自2021年新高考Ⅰ卷考查后就开始成为了一个考查热点，之后各地的模拟题也出现了不少相关试题.本文中以两道高考真题为例谈
解题天地 | 齐次化思想在解析几何中的应用

解题天地 | 齐次化思想在解析几何中的应用

数学运算是数学核心素养之一.运算过程的繁与简，结果能否正确呈现，反映了学生运算能力的高低.不同的方法选择，运算的难易程度往往差别较大.这正是教师要教会学生的地方.如何去突破运算瓶颈？怎样选择解题方法？为什么这么选？要用到什么技巧？需要多总结体会，做到心中有底，手中有法. 1 运算的难点与解决策略高三解析几何的复习教学中，常会遇到像斜率之和、斜率之积为常数，定点、定值等问题.对于这类问题，基础
解题天地 | 运用割补法解题的五种技巧

解题天地 | 运用割补法解题的五种技巧

摘要：立体几何中，割补法在求面积和体积类的问题中有着广泛的应用.在解题过程中若能巧妙地对几何体实施“割”或“补”，就能变整体为局部、化不规则为规则，有利于找到解决问题的突破口，快速解决问题.本文中结合实例给出了五种解题技巧，即补“台”为“锥”巧求值，切割补形巧证明，补“柱”为“体”巧代换，补“形”转化求距离，补“锥”为“柱”求体积. 关键词：割补法；解题技巧 “割”，就是把不规则的几何图形分割
解题天地 | 放缩法处理零点存在定理中的找点问题

解题天地 | 放缩法处理零点存在定理中的找点问题

摘要：零点存在定理中的找点问题一直是导数压轴题中的难点，文章对近年来各地高考题中的此类问题进行了深入探究，对“特殊点”的来龙去脉追本溯源，并归纳总结了几种常见的找点方法. 关键词：放缩法；零点；找点零点存在定理：如果函数y=f（x）在区间［a，b］上的图象是一条连续不断的曲线，并且有f（a）f（b）<0，那么函数y=f（x）在区间（a，b）内至少有零点，即存在x0∈（a，b），使得f（
解题天地 | 一道高考数列题的解法探究

解题天地 | 一道高考数列题的解法探究

摘要：求解数列的通项公式和前n项和公式，是数列内容考查的重点.求数列通项公式的方法主要有累加法、累乘法、构造法、待定系数法和数学归纳法等.求数列前n项和的方法主要有公式法、分组求和法、错位相减法、裂项相消法等.文章通过探究一道高考题，给出了该题求解数列通项公式与前n项和公式的四种解法. 关键词：数列；通项公式；前n项和公式；解法探究数列大题是高考必考的题型，主要涉及数列的通项公式、前n项和以
解题天地 | 高中数学“函数的概念与性质”解题分析

解题天地 | 高中数学“函数的概念与性质”解题分析

摘要：在教育教学的不断改革背景下，高中数学教学要开放思路，重视对学生多种能力的培养，特别是对学生解题能力的培养要加大力度和强度，因为培养学生的解题能力也是在培养学生的创新能力.本研究中，以函数的概念与性质相关内容为例进行了几种解题方法的探讨. 关键词：高中数学；函数的概念与性质；学生进入到高中阶段，数学学习变得有一些难度，特别是一些数学问题的解决，如果不能掌握有效的方法，则会比较吃力.在高中
解题天地 | 利用对称思想，巧解概率问题

解题天地 | 利用对称思想，巧解概率问题

摘要：对称思想在解决一些数学问题中有奇效，是充分挖掘题目条件内涵基础上的灵活应用思想.而借助对称性来解决与概率有关的数学问题，特别是对于随机事件概率的计算、数学期望的应用、正态分布的应用等方面，对称性是一种特殊的技巧与方法.本文中结合实例，就对称性思维解决概率问题的常规方法与对称法加以比较，实现解题的最优化. 关键词：对称思想；概率；计算；数学期望对称思想是借助数的结构属性或形的几何
解题天地 | 一道三角最值题的探究

解题天地 | 一道三角最值题的探究

摘要：三角函数的综合应用问题，立足函数本质，融合其他众多的相关数学知识，成为各类试题中命题的一个重要场景.借助一道三角函数最值题的剖析，从多个数学思维视角入手，合理一题多解，巧妙追根溯源实现试题链接，开拓数学思维进行变式拓展. 关键词：三角函数；最值；不等式；函数；导数；几何涉及三角函数代数式的综合应用问题，基于三角函数模块知识，如三角函数的定义、三角恒等变换及三角函数的图象与性质等
解题天地 | 立足三角函数本质，交汇函数方程内涵

解题天地 | 立足三角函数本质，交汇函数方程内涵

摘要：三角函数问题是基于函数与方程问题的拓展与应用，二者之间的交汇与融合更是高考中比较常见的基本题型之一.本文中结合一道涉及两个三角函数的图象在给定区间上公共点个数，进而来确定对应参数的取值范围题，从不同思维视角切入，通过不同技巧、方法来解决，合理拓展变式，归纳总结规律，有效避免“题海战术”，真正做到开拓数学思维，培养数学素养. 关键词：三角函数；图象；函数与方程；解析几何；特殊值三
解题天地 | 依托数列应用，回归函数本质

解题天地 | 依托数列应用，回归函数本质

摘要：数列的函数性是数列中一个本质的基本属性，作为函数知识体系的一个分支，数列自身有独特的内涵与实质.结合一道高考数列题的展示，借助不同的思维方法进行分析与应用，巧妙利用数列的基本公式及数列的函数性等相关思维来切入与应用，合理优化解题过程与变式拓展，有效指导复习备考. 关键词：高考；数列；公式；函数；变式数列是《普通高中数学课程标准（2017年版2020年修订）》选择性必修课程中函数
解题天地 | 一道强基复数试题的探究

解题天地 | 一道强基复数试题的探究

摘要：复数作为高考数学与强基命题中的一个基本考点，往往难度中等偏下，而其涉及的基础知识与基本技能是命题与考查的一个重要方向.结合一道复数强基题，挖掘问题的内涵，从三角思维、不等式思维及几何思维等不同形式切入，强化逻辑推理与数学运算能力，引领并指导数学教学与复习备考. 关键词：复数；最小值；三角；不等式；几何涉及复数的基本运算、基本性质与模的综合应用问题，是复数模块知识考查的一个基本点
教师发展 | 新高考背景下减少死记硬背和机械刷题的思考

教师发展 | 新高考背景下减少死记硬背和机械刷题的思考

摘要：在新高考背景下，减少死记硬背和机械刷题的教学方式对于提升学生的综合素质和应对能力至关重要.本文中首先剖析了死记硬背和机械刷题现象的形成背景，指出其在新高考及能力培养方面的不足.接着，通过实例展示了仅依赖死记硬背和机械刷题无法有效应对新的育人及考试要求.最后，探讨了通过强调理解和应用、培养创新思维、采用多样化的教学方法和个性化教学等措施来减少死记硬背和机械刷题的思考. 关键词：新高考；死记硬
教师发展 | “本手”筑基，“妙手”生花

教师发展 | “本手”筑基，“妙手”生花

摘要：从围棋术语的“本手、妙手、俗手”展开并切入，合理应用到数学教学与解题研究过程中去，结合一道模拟题的实例解析，阐述数学解题“本手”与“妙手”的基本策略技巧，从数学本质、数学思维等不同层面进行拓展与深化，指导解题研究与复习备考. 关键词：本手；妙手；最小值；基本不等式 2022年全国高考语文新高考I卷的作文题围绕“本手、妙手、俗手”这三个围棋术语来切入与展开，极具创新性与应用性.其中
教师发展 | “一题多问”之圆锥常考问题剖析

教师发展 | “一题多问”之圆锥常考问题剖析

从几何体的分类角度看，圆锥属于简单旋转体，将直角三角形绕着它的一条直角边所在直线旋转一周，即可得到圆锥.关于圆锥常考问题，本文中拟通过“一题多问”的方式加以具体剖析，旨在帮助学生理清常用解题思维方法，提高空间想象能力以及运算求解能力. 1 一题多问（原创题）如图1，已知圆锥的顶点为S，底面圆心为O，AB为底面圆的直径，且圆锥的母线长l=3，底面圆的半径r=1. （1）求圆锥的体积、侧面积和
教师发展 | 立体几何中的探索性问题探析

教师发展 | 立体几何中的探索性问题探析

摘要：探索性问题是近年来高考立体几何中的常见题型，常以动点形式出现.探索性问题主要是对位置关系、角的大小以及点的位置的探究，或者对条件和结论不完备的开放性问题的探究.解决此类问题时，通常先根据探索性问题的设问，假设其存在并探索出结论，然后在这个假设下进行合情合理的推理与论证，若得到合乎情理的结论就肯定假设，若得到矛盾就否定假设. 关键词：立体几何；探索性；问题探索性问题是近年各种考试

逻辑星辉映思维，推理探究启新知
二面角的概念与二面角的平面角教学
情境丰富问题驱动教书育人
如何把教科书中的数学问题转变为建模问题
椭圆的一个“小题大做”的优美结论
层层剖析，激发学生的创造力
融入数学文化，探究体积应用
关于平面无限延展性的教学思考
注重类比思维，聚焦核心素养
素养立意下高中数学学能课程教学模式建构与应用策略研究
“创艺”融合理念下“函数的概念”教学设计
素养为本的重组单元“承启”课教学研究
借助情景燃点启动思维火花
基于GeoGebra的高中数学可视化教学
在反省中激活学生的数学直觉思维
数列与其他知识点的交汇融合
嵌套函数的零点问题刍议
谈高三复习中解题思路的建立和形成
挖掘特征巧换元，最值求解妙突破
圆锥曲线中斜率和（积）的定值与定点问题
依托复数几何意义，巧妙解决应用问题
三角函数周期确定的“四法”技巧
立几体积巧求解，分割补形总相宜
立足典型问题，优化复数运算，发散思维应用
基于高考评价体系的近两年新高考Ⅰ卷数列试题分析
整体剖析话全局，细节切入详分析
基于难度模型的近两年新高考Ⅰ卷解几试题分析及教学启示
追踪高考脉络探寻方法本质
自主编题促提高
一类高考导数真题的探究及新题命制
基于2022年甲卷圆锥曲线压轴题的原创题命制
社会生活情境下的数学抽象素养三种水平试题赏析及命题启示
巧借三角形全等条件，妙设未知量解三角形
数形结合思想巧解题，对数函数图象妙应用
依托指数函数图象，数形结合解决问题
2023年全国高考数学I卷第17题13解
巧用思维导图优化解题教学
公切线场景设置，巧思维与妙拓展
常规三角变换，特殊思维应用
高考分段数列试题的解法探究与变式教学
齐次化思想在解析几何中的应用
运用割补法解题的五种技巧
放缩法处理零点存在定理中的找点问题
一道高考数列题的解法探究
高中数学“函数的概念与性质”解题分析
利用对称思想，巧解概率问题
一道三角最值题的探究
立足三角函数本质，交汇函数方程内涵
依托数列应用，回归函数本质
一道强基复数试题的探究
新高考背景下减少死记硬背和机械刷题的思考
“本手”筑基，“妙手”生花
“一题多问”之圆锥常考问题剖析
立体几何中的探索性问题探析

过往期刊

更多

中学数学·高中版
2025年04期
中学数学·高中版
2025年03期
中学数学·高中版
2025年02期
中学数学·高中版
2025年01期

猜你喜欢

兴趣阅读·少年诗刊
2025年04期
学习方法报·读写拍档新高考版
2025年50期
学习方法报·读写拍档高中版
2025年50期
学习方法报·政治新高考版新教材
2025年48期
学习方法报·历史新教材高一
2025年48期
学习方法报·政治新教材高二
2025年48期
学习方法报·写作（高二）
2025年48期
学习方法报·历史新高考版新教材
2025年48期

Copyright © 2017 龙源数字传媒集团京ICP备060024号
Dragonsource.com Inc. All Rights Reserved
IP:3.137.222.1

上海外国语大学电子阅览室

首页
全部分类
排行榜
客户端下载

登录
个人中心我的收藏退出登录
简体 / 繁体

上海外国语大学电子阅览室

忘记密码新用户

新用户注册

已有账户

注册成功

修改电子邮件