目录
快速导航-
教学纵横 | “双减”背景下高中数学大单元作业设计实践
教学纵横 | “双减”背景下高中数学大单元作业设计实践
-
教学纵横 | 大概念视域下的高中数学单元作业设计探究
教学纵横 | 大概念视域下的高中数学单元作业设计探究
-
教学纵横 | 融入数学文化 助力概念教学
教学纵横 | 融入数学文化 助力概念教学
-

教学纵横 | 凸现主体地位,促进深度学习
教学纵横 | 凸现主体地位,促进深度学习
-

教例探微 | “尊重学生想法”的教学才是“有效的教学”
教例探微 | “尊重学生想法”的教学才是“有效的教学”
-

教例探微 | 基于素养培养发展学习能力
教例探微 | 基于素养培养发展学习能力
-

教例探微 | 在“三新”背景下应重视课本习题的合理使用
教例探微 | 在“三新”背景下应重视课本习题的合理使用
-
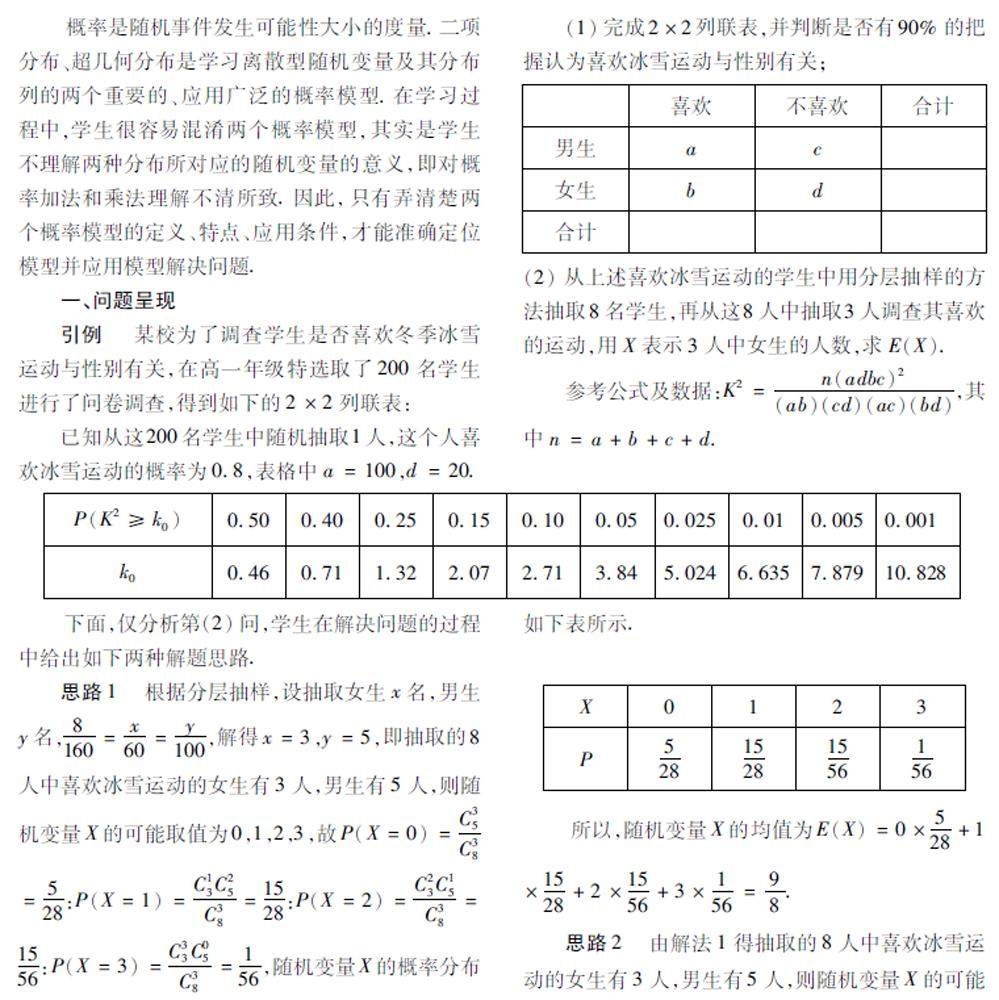
教例探微 | 超几何分布与二项分布的辨析与应用
教例探微 | 超几何分布与二项分布的辨析与应用
-

聚焦高考 | 批判思维培养视角下的试题课堂讲解路径探究及教学启示
聚焦高考 | 批判思维培养视角下的试题课堂讲解路径探究及教学启示
-

聚焦高考 | 一道高考概率问题的多解探究与变式
聚焦高考 | 一道高考概率问题的多解探究与变式
-

聚焦高考 | 数学思想方法视域下高考立体几何试题评析与备考策略
聚焦高考 | 数学思想方法视域下高考立体几何试题评析与备考策略
-

聚焦高考 | 圆锥曲线一轮复习的备考策略与建议
聚焦高考 | 圆锥曲线一轮复习的备考策略与建议
-

专题研究 | 一个几何不等式的新证法与加强
专题研究 | 一个几何不等式的新证法与加强
-

专题研究 | 两道关于三角形高线和征解问题的改进
专题研究 | 两道关于三角形高线和征解问题的改进
-

专题研究 | 一道最值问题的同构解法探究与变式
专题研究 | 一道最值问题的同构解法探究与变式
-

专题研究 | 一道抛物线中四点横坐标乘积为定值问题的探究
专题研究 | 一道抛物线中四点横坐标乘积为定值问题的探究
-

专题研究 | 仿射变换之化“椭”为“圆”的应用
专题研究 | 仿射变换之化“椭”为“圆”的应用
-

解题方法与技巧 | 一道函数值域问题引发的思考
解题方法与技巧 | 一道函数值域问题引发的思考
-

解题方法与技巧 | 一道函数不等式的证明及模型建构
解题方法与技巧 | 一道函数不等式的证明及模型建构
-

解题方法与技巧 | 圆锥曲线中的定值、定点定线问题的破解策略
解题方法与技巧 | 圆锥曲线中的定值、定点定线问题的破解策略
-

解题方法与技巧 | 活跃在中考试题中的“赵爽弦图”
解题方法与技巧 | 活跃在中考试题中的“赵爽弦图”
-

竞赛之窗 | 一个优美代数不等式及其在竞赛中的应用
竞赛之窗 | 一个优美代数不等式及其在竞赛中的应用
-

竞赛之窗 | 数学竞赛中的四点共圆问题研究
竞赛之窗 | 数学竞赛中的四点共圆问题研究
















 登录
登录