全部分类/
教育教学/
语数外学习·高中版下旬

语数外学习·高中版下旬

2024年06期

《语数外学习》杂志1985年创刊，由湖北第二师范学院主管,湖北第二师范学院主办的优秀教育类期刊。

扫码免费借阅

目录

快速导航

卷首文萃 | 春的歌

卷首文萃 | 春的歌

丁香花，你是什么时候开放的？莫非是我前日为了她，为她哭泣的时候？海棠的花蕾，你是什么时候生长的？莫非是我为了她的憧影，敛去了愁容的时候？燕子，你是什么时候来到的？莫非是我昨夜相思，相思正浓的时候？丁香、海棠、燕子，我还是想啊，想为她唱些“春的歌”，无奈已是暮春的时候。
语文 | 《喜看稻菽千重浪》的教学策略分享

语文 | 《喜看稻菽千重浪》的教学策略分享

《喜看稻菽千重浪 — —记首届国家最高技术奖获得者袁隆平》是新版高中语文教材必修上册第二单元的一篇课文。作者通过记录典型的事件，介绍了袁隆平院士发现天然杂交水稻、培育杂交水稻和选育“超级水稻”的艰难历程，歌颂了科学家高度的责任心和可贵的科学精神。针对《喜看稻菽千重浪 — —记首届国家最高技术奖获得者袁隆平》，我们可以引导学生梳理作者的行文思路，学习其中的写作方法，探究作品的主题。具体的教学过程如下
语文 | 怎样读懂句子的“言外之意”

语文 | 怎样读懂句子的“言外之意”

阅读实际上是一种通过视觉接收信息，调动人的多种感官，对文本的内容进行再认识、再加工和再创造的过程。我们在阅读文章的时候一般需要先理解字、词、句、段的意思，再逐步去理解整篇文章的内涵。整个阅读的过程一般需要经过“阅读文本（理解大意）—分析结构（把握全篇）—总结内容（归纳主旨）—研究语法（探讨技巧）—找出特色（判定高低）”等多个阶段。而“阅读文本（理解大意）”就是阅读的起始阶段。当然，理解文本的大
语文 | 谈谈烛之武是如何劝退秦军的

语文 | 谈谈烛之武是如何劝退秦军的

兵临城下，郑国危若累卵，烛之武临危受命，凭三寸不烂之舌劝退了强秦的军队，迫使晋国不得不“亦去之”。其过人的胆识和口才让人不由得心生钦佩之情。那么，烛之武是如何劝退秦军的呢？一、单刀直入烛之武知道自己此行责任重大，若是不能完成使命，国家便免不了要经历一场浩劫。那么，如何才能达到目的呢？烛之武肯定经过了一番深思熟虑。他知道秦、郑两国之间本来并没有什么尖锐的矛盾冲突。秦国协助晋国攻打郑国，无非是
语文 | 《边城》中的四类情感简析

语文 | 《边城》中的四类情感简析

1931年，中国社会正处在表面平静、内里暗流涌动的特殊时期，《边城》便创作于此年。当时，沈从文正处在爱情、事业双丰收的幸福时期，在探讨人性的本质的同时，希望通过描述自己记忆中的故土湘西，搭建一个“乌托邦式”的世界，为在都市文明中感到迷茫的人指引人生的方向，并以此告诫世人：人间尚有纯洁、自然的真情。下面，笔者就简要分析一下《边城》中的各类情感。一、祖孙情在《边城》中，作者详细地交代了小说的主
语文 | 聚焦单元主题，开展单元教学

语文 | 聚焦单元主题，开展单元教学

在单元教学中，我们要遵循新课标的要求，针对整个单元的课文进行统一的教学。新版高中语文教材是按照主题来选文和编排的。这为我们开展单元教学打下了基础。在开展单元教学之前，教师首先要对整个单元的内容进行分析，提炼出本单元的主题，再结合主题对教学内容进行梳理，从整体出发，设计合适的教学方案。下面，笔者就以小说单元的课文为例，谈谈如何开展单元教学。一、提炼单元主题，确定教学方案新版高中语文教材选编了
语文 | 开展“选曲填词”活动，带领学生感受语言文字的美

语文 | 开展“选曲填词”活动，带领学生感受语言文字的美

审美鉴赏与创造是语文核心素养中非常重要的一个部分。在平时的阅读教学中，我们常常关注学生是否读懂了课文，是否掌握了知识，容易将鉴赏课变为单纯的“说文解字”题的解答。笔者认为，这样做无法满足学生个性化的学习需求，无法真正让他们感受到课文的美。对此，我们可以适时创新，开展“选曲填词”活动，带领他们感受课文的美。一、开展“选曲填词”活动的原因拆解文段、词句，引导学生解读文本是我们在语文课上时常做的
语文 | 浅谈文言文中常见的四类句式

语文 | 浅谈文言文中常见的四类句式

文言文翻译题是语文考试必考的题型之一。一些同学在做这一题时经常丢分。这主要是因为大家没有掌握相应的基础知识。下面，笔者就带领同学们回顾文言文中的四大句式，希望可以帮助大家巩固基础知识。一、判断句判断句一般是对客观事物的性质、现象、情况等作出肯定或否定回答的句子。与现代汉语不同的是，古代汉语中几乎不使用“是”或“不是”这类具有判断性质的词语，而是以名词、代词或名词短语作为谓语来加以判断，并与
语文 | 《谏逐客书》的论证方法探究

语文 | 《谏逐客书》的论证方法探究

《谏逐客书》是西汉文学家李斯所写的一篇文章。在文章中，他劝谏秦王收回驱逐客卿的政令，强调了客卿对秦国的贡献和重要性。在文章中，作者所用的论证方法值得我们学习。下面，笔者就逐一谈谈。一、通过对比进行论证李斯通过将秦国与其他国家进行对比来强调客卿对于秦国的重要性。他指出，秦国与其他国家相比，具有强大的实力，占据着优越的地理位置。但是秦国能取得这些成就是离不开客卿的帮助的。例如，秦国的军队武
语文 | 简析提出“无效问题”的原因及应对策略

语文 | 简析提出“无效问题”的原因及应对策略

在教学中，我们应当以促进学生的全面发展为目标，在帮助他们培养必备品格和关键能力的同时，强化其主体地位。我们要参照“新课标”中的内容，及时更新育人理念，改变教学方式，由以教为主向以学为主转变，打造新时代需要的语文课堂，在立德树人方面充分发挥语文课程的育人作用，彰显语文学科的独特优势。在语文课上，我们通过提问可以很好地调动学生的学习积极性，培养其思维能力，全面提升他们的语文核心素养。但是，我们有时候提
语文 | 如何指导学生围绕材料来拟题

语文 | 如何指导学生围绕材料来拟题

古语有云： “题者，额也；目者，眼也。”这句话的意思是文章的题目好似人的“额”与“眼”，有着极其重要的作用。的确， “看书先看皮，看文先看题”。作文的题目贴切醒目、新颖别致，确实能给阅卷老师以耳目一新、怦然心动的感觉；如果题目平庸乏味，甚至与材料无关，将会直接影响文章的得分。可见，在拟题时务必要谨慎。新材料作文题不同于以往的材料作文题，它往往会给出一段或几段材料。材料的内容要么是古今故事，要么
数学 | 函数思想在解答数学问题中的应用

数学 | 函数思想在解答数学问题中的应用

函数思想是高中数学中的重要思想，在解题中应用广泛.在高中数学教学中，教师要注意渗透函数思想，帮助学生掌握函数思想的特点、应用方法、适应范围等，并学会灵活运用函数思想来解题.那么如何运用函数思想来解题呢？下面结合实例进行探讨. 一、函数思想在解答集合问题中的应用有些集合问题中涉及了反比例函数式、一次函数式、二次函数式、幂函数式、指数函数式、对数函数式等，此时学生可以将集合中约束元素的关系式视为
数学 | 例谈用点差法求解中点弦问题的思路

数学 | 例谈用点差法求解中点弦问题的思路

中点弦问题是指与圆锥曲线的弦的中点有关的问题.这类问题侧重于考查直线与圆锥曲线的位置关系，以及直线的斜率公式、中点坐标公式、直线的方程等的应用.常见的中点弦问题有：（1）求中点弦所在直线的方程、斜率；（2）求圆锥曲线的方程；（3）求中点弦的坐标.而点差法是解答中点弦问题的常用方法. 本题中，线段 AC 的垂直平分线将弦 AC 平分，则垂直平分线与弦的交点为弦的中点，那么本题实质上就是中点弦
数学 | 对一道三角函数零点问题的解法的探究

数学 | 对一道三角函数零点问题的解法的探究

解答三角函数零点问题，需抓住函数零点的定义：函数 y=f （ x）的零点即为 f （ x）=0 时x的取值，也是函数y=f （ x）与x轴的交点的横坐标，从方程和函数图象入手来寻找解题的思路.对于由三角函数的零点求参数的取值范围问题，可以运用方程思想和数形结合思想来解题.下面结合实例进行探讨. 例题：（2023年高考新课标数学Ⅰ卷，第15题）已知函数 f （ x）=cosωx-1 （）
数学 | 怎样证明有关抛物线切线的四个重要结论

数学 | 怎样证明有关抛物线切线的四个重要结论

有关抛物线的切线问题经常出现在各类试题中.这类问题的运算量较大，且解题过程繁琐，于是笔者对一些常见的、典型的有关抛物线切线的问题进行了总结，然后将其推广得到一般的情形，得到如下的四个结论. 该结论适用于解答过抛物线准线上一点的切线的斜率问题.该结论的适用范围较窄. 在解答选择、填空题时，我们可以直接将这四个结论应用于解题中，即可快速获得问题的答案.同学们要熟练掌握有关抛物线的切线的这四个结论，
数学 | 求解二元最值问题的三种路径

数学 | 求解二元最值问题的三种路径

二元最值问题具有较强的综合性，常与导数、方程、三角函数、不等式、函数等知识相结合.此类问题对同学们的分析以及运算能力有较高的要求.解题的关键在于如何处理两个变量之间的关系，求得最值.那么解答二元最值问题有哪些路径呢？这里主要介绍三种路径. 可见，利用基本不等式、判别式，通过三角换元，可以将两个变量的和与积关联起来，也可以将两个变量用一个变量表示出来，这样便能达到化繁为简、化难为易的目的. （作
数学 | 导数法 ——解答函数问题的“利器”

数学 | 导数法 ——解答函数问题的“利器”

导数法是运用导数知识解答问题的方法.导数法是解答函数问题的重要方法，尤其在解答函数单调性问题、图象问题、最值问题、不等式问题时，灵活运用导数法，可化难为易、化繁为简.那么如何巧妙运用导数法来解答函数问题呢？下面结合实例进行探讨. 一、函数单调性问题函数单调性问题的常见命题形式有：（1）判断函数的单调性；（2）求函数的单调区间；（3）由函数的单调性求参数的取值范围.对于简单的函数单调性问
数学 | 如何解答直线与圆锥曲线问题

数学 | 如何解答直线与圆锥曲线问题

直线与圆锥曲线问题经常出现在圆锥曲线试题中.这类问题的主要特点是题型多变、综合性强、计算量大.常见的直线与圆锥曲线问题有：弦长问题、中点弦问题、最值问题.下面将结合实例，对直线与圆锥曲线的三类题型及解法展开讨论.
数学 | 灵活运用特殊值法，提升解答选择题的效率

数学 | 灵活运用特殊值法，提升解答选择题的效率

解答选择题，往往不需要提供详细的解题过程，只要求选出满足题意的选项.那么，在解答选择题时，我们就不需要花费大量的时间和精力去研究解题的详细过程，只需根据题意选取一些满足题意的特殊值、特殊点、特殊角、特殊位置、特殊函数、特殊数列、特殊方程、特殊模型等，将其代入题设中进行计算、推理，即可快速得出结论.这样不仅能减少运算量，简化解题的过程，还能提升解题的速度.
数学 | 由一道三角形取值范围问题引发的思考

数学 | 由一道三角形取值范围问题引发的思考

三角形的取值范围问题具有较强的综合性，常与三角函数、解三角形、不等式、函数、向量等知识相结合.这类问题的命题形式多种多样，解题方法也各不相同.本文通过一道三角形取值范围问题，探讨一下求解此类问题的思路.
数学 | 一道三棱锥体积问题的多种解法

数学 | 一道三棱锥体积问题的多种解法

三棱锥体积问题主要考查三棱锥的体积公式、性质，线面垂直的判定定理，线面平行的性质定理等.笔者从多个角度探索了一道三棱锥体积问题的解法，并对其进行了总结归纳.
数学 | 巧换元，妙解代数题

数学 | 巧换元，妙解代数题

换元是指将原来结构复杂、关系不明朗的量用新变量替换，从而使代数式得以简化.运用换元法，可以将复杂的问题简单化，将陌生的问题变为我们所熟悉的问题.换元主要包括三角换元、均值换元、比值换元、整体换元等.本文主要谈一谈如何巧妙地运用换元法求解代数式问题.
数学 | 选用合适的方法，快速求得函数的最值

数学 | 选用合适的方法，快速求得函数的最值

函数最值问题通常要求在定义域内寻找函数的最大值和最小值.解答这类问题的方法有很多种，比如换元法、基本不等式法、数形结合法、导数法等.本文主要谈一谈，如何运用换元法和基本不等式法求函数的最值. 一、换元法对于较为复杂的函数式，如含有复合函数、根式、绝对值的函数式，通常需采用换元法来将函数式化简，以便根据简单基本函数的性质求得函数的最值.换元主要包括整体换元、局部换元、三角换元、均值换元.在解题
数学 | 谈谈证明数列不等式的途径

数学 | 谈谈证明数列不等式的途径

证明数列不等式问题的命题形式多样，解法灵活.这类问题的难度一般较大，很多同学在面对此类问题时不知该如何下手.下面，笔者介绍两种证明数列不等式的“途径”，供大家参考. 一、通过裂项相消证明不等式当题目中的数列为分式、根式、对数式时，我们通常可以将数列的各项进行裂项，使其成为两项之差的形式，那么将各项相加时，互为相反数的两项便会相互抵消，即可通过裂项相消快速求得数列的和.最后对和式进行适当的放缩
数学 | 破解极值点偏移问题的两个“妙招”

数学 | 破解极值点偏移问题的两个“妙招”

一、构造对称函数运用此方法解答极值点偏移问题，首先要对函数求导，根据极值的定义求得函数极值点的表达式；然后将x 1 、x 2 的关系式变形，使得x 1 、x 2 分别在不等号或等号的两侧；再根据极值点的表达式构造出对称函数式，如F（ x）=f （ x 0 -x）-f （ x 0 +x）；最后讨论新构造的函数的单调性，得到与x 1 、x 2 相关的新关系式，即可证明结论.
数学 | 怎样解答三角函数求值问题

数学 | 怎样解答三角函数求值问题

三角函数求值问题的难度不大，常以选择题、填空题的形式出现.常见的命题形式是：根据已知条件求某个角的大小、某个角的三角函数的值及其关系式.这类问题通常会重点考查同学们对三角函数的定义、公式、性质及图象的掌握情况.下面来探讨一道题目的解法.
数学 | 例说函数凹凸性的应用技巧

数学 | 例说函数凹凸性的应用技巧

对于函数的凹凸性，教材中没有给出明确的定义，只是以练习题的形式点到为止.然而在平时的训练和高考试题中，函数的凹凸性却有着广泛的应用.对此，笔者就函数凹凸性的应用技巧进行了深入的探讨.下面主要谈一谈如何运用函数的凹凸性求函数的极值和求解函数的图象问题. 一、求函数的极值对于求函数 f （） x 的极值问题，我们习惯性地对函数求导，再求出 f′ （） x ≥0和 f′ （） x ≤0时的x
数学 | 求解三角形周长最值问题的两种措施

数学 | 求解三角形周长最值问题的两种措施

三角形问题常与解三角形、三角函数、不等式、向量、平面几何等知识相结合.因而解答三角形周长的最值问题，可以从多个知识点入手来寻找解题的思路.下面结合一道例题，谈一谈求解三角形周长最值问题的措施.
数学 | 三类函数问题的解法剖析

数学 | 三类函数问题的解法剖析

函数问题比较常见，这类问题侧重于考查一次函数、二次函数、幂函数、指数函数、对数函数等基本初等函数的定义、图象、性质的应用.常见的函数问题有：函数运算问题、函数图象问题、函数性质问题、函数应用问题等.下面结合例题谈一谈三类函数问题的解法. 一、函数运算问题函数运算问题侧重于考查幂函数、指数函数、对数函数的运算.解答函数运算问题，不仅需熟记并灵活运用幂函数、指数函数、对数函数的运算法则和性质，还
数学 | 抓住数列的特点，求其通项公式

数学 | 抓住数列的特点，求其通项公式

数列的通项公式是数列中的重要内容.我们知道，等差数列的通项公式为 a n =a 1 + （） n-1 d ，等比数列的通项公式为 a n =a 1 qn-1 .有些数列的通项公式问题较为复杂，需根据数列的递推式求数列的通项公式，这就需要运用一些求数列通项公式的技巧、方法.下面结合例题，谈一谈求数列通项公式的几个技巧. 一、引入待定系数对于同时含有 a n+1 、a n 、a n-1 的递推式
数学 | 《直线和圆》专题训练

数学 | 《直线和圆》专题训练

一、单选题 1. 若直线 2x+y-1=0 是圆（ x-a ）2+y 2 =1 的一条对称轴，则 a= （）.
英语 | 采用互动教学模式，提高阅读教学的效率

英语 | 采用互动教学模式，提高阅读教学的效率

许多英语教师只是将“互动”简单地理解为教师与学生之间的简单问答，既没有创新互动的形式，也没有丰富与学生交流的内容，从而导致互动没有达到其应有的效果。为此，文章将从师生互动、生生互动、生本互动三个角度，探讨互动式教学模式在高中英语阅读教学中的具体运用方法。一、师生互动，激发学生的阅读期待学生是否能对将要学习的内容产生学习期待将很大程度上影响他们的学习效果。为此，教师可以在导入环节，将文本内容
英语 | 谈谈阅读理解题和写作题的类型及备考建议

英语 | 谈谈阅读理解题和写作题的类型及备考建议

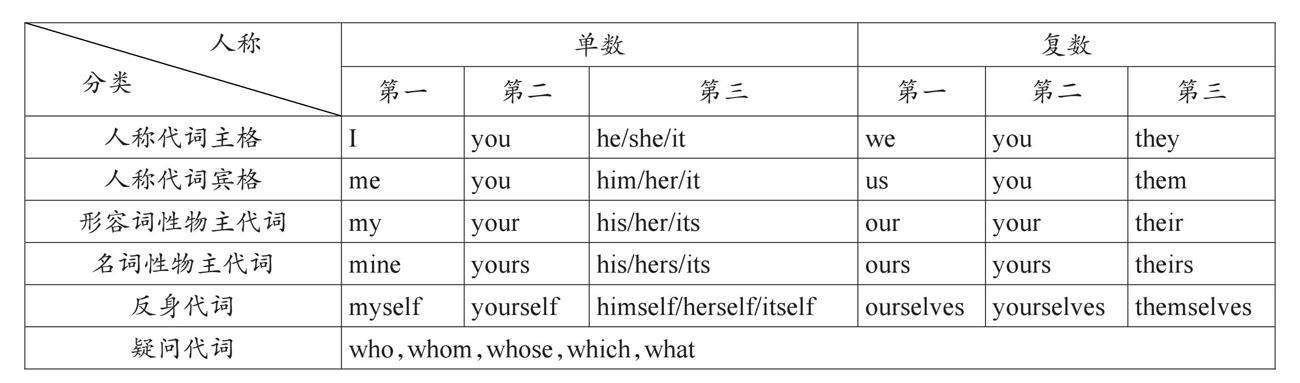
高考在贯彻党的教育方针，落实立德树人的根本任务方面一直担任“风向标”的角色。2023年高考英语全国乙卷依然坚持以“立德树人、服务选才、引导教学”为核心功能，引导教师、学生重视核心价值，提高学科素养，培养关键能力并储备必备知识，努力做到德智体美劳全面发展。与此同时，考查的基础性、综合性、应用性和创新性也在今年的试题中得到了充分体现。纵观全卷，2023年高考英语全国乙卷的试题与高考评价体系的“一核四层
英语 | 例析有关代词的几个考点

英语 | 例析有关代词的几个考点

高中英语考试除了考查在具体语境中代词的用法外，还经常考查不同代词的区别。在解题的过程中，同学们一定要注意明晰有关代词的考点，以提升解题能力。一、有关人称代词、物主代词、反身代词与疑问代词的考点根据代词的类型，高中阶段常考到的人称代词、物主代词、反身代词与疑问代词包括如下几种：上述代词的出题方式通常比较单一，多是考查代词在具体文章中的用法。高中阶段，上述代词常涉及的考点以及易错点包括： 1
英语 | 过去分词的几种易混用法剖析

英语 | 过去分词的几种易混用法剖析

我们知道，过去分词、动词不定式、现在分词和动名词一起同为非谓语动词的四种基本形式。在这四种基本形式中，虽然过去分词的形式只有一种，看似简单。但是实际上，由于过去分词在句子中的句法功能较多，学习的难度较大。笔者将结合近几年高考英语试题中涉及过去分词用法的真题，针对同学们在这个语法项目上的常见易错点进行分析探究，以期对同学们的学习有所帮助。一、过去分词作状语时与现在分词的混淆点【高考链接】（2
英语 | 表语从句的用法归纳

英语 | 表语从句的用法归纳

表语从句与主语从句、宾语从句和同位语从句一起统称为名词性从句。文章将结合平时学生在学习表语从句时容易出现的错误，以高考试题中表语从句的真题为例，来分析表语从句的用法，从而帮助学生正确运用表语从句。一、what与that引导表语从句【高考链接】（2018·北京）15. This is _________my father has taught me—to always face diffic
英语 | 使用特殊句式时的易错点分析

英语 | 使用特殊句式时的易错点分析

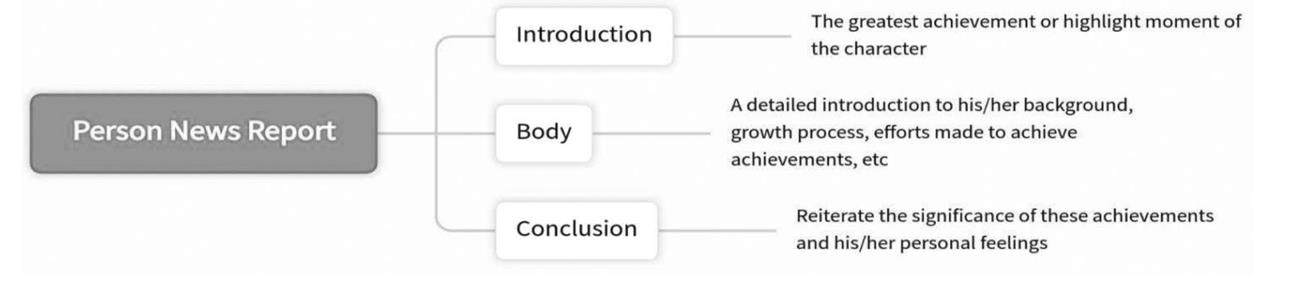
在高中英语学习中，我们会遇到这样的一些英语句子：它们的句子结构与我们常见的简单句的基本句型的结构存在着或多或少的区别，我们称含有这样结构的句子为特殊句式。英语中常见的特殊句式主要包括强调句、倒装句、祈使句、省略句、感叹句、反意疑问句和there be句型等。在近几年高考英语试题中，我们都可以看到这些特殊句式的身影。同时，随着新高考的写作题又增加了读后续写题这种写作类型，如果同学们能把含有特殊句式的
英语 | 开展仿写训练，提高学生的写作能力

英语 | 开展仿写训练，提高学生的写作能力

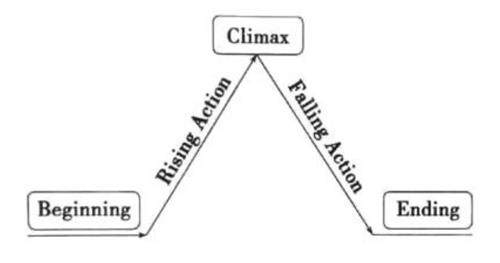
在英语教学中引导学生开展仿写训练是以教材为依托，让学生在熟悉的语境中进行创作，降低写作的难度，从而激发学生的写作兴趣。本文旨在探讨在高中英语教学中如何引导学生开展仿写训练，以便提高学生的写作能力。一、在仿写前引导学生分析范文框架在开展仿写训练前，教师需要根据学生的实际水平和教学目标选择合适的仿写文本。在选择了合适的仿写文本之后，教师需要带领学生分析范文的结构，让学生了解作者的写作思路和文本
英语 | 怎样在读后续写教学中做到“教—学—评”一体化

英语 | 怎样在读后续写教学中做到“教—学—评”一体化

传统的高中英语教学模式缺乏互动性，学生参与度低，而现代英语教学模式的发展趋势是朝向引导学生进行个性化学习、合作学习、反思性学习等方面发展。这种趋势的出现旨在提供更灵活、富有互动性和培养学生综合能力的教学环境，以更好地满足学生的学习需求和培养学生的终身学习能力。本课题研究的目的是为了解决高中英语教学中存在的问题，其研究的意义在于提供一种具有实践效果的教学模式，为高中英语教育改革提供有益的经验和启示。

过往期刊

更多

猜你喜欢

上海外国语大学电子阅览室