全部分类/
教育教学/
中学数学·高中版

中学数学·高中版

2025年04期

扫码免费借阅

目录

快速导航

特色展台 | 2024年上海高考第21题的探究

特色展台 | 2024年上海高考第21题的探究

1 题目（2024年上海第21题）对于一个函数f（x）和一个点M（a，b），令s（x）=（x-a）2+（f（x）-b）2，若P（x0，f（x0））是s（x）取到最小值的点，则称P是M在f（x）的“最近点”. （1）对于f（x）=1x（x>0），求证：对于点M（0，0），存在点P，使得点P是M在f（x）的“最近点”. （2）对于f（x）=ex，M（1，0），请判断是否存在一个点P，它是
特色展台 | 回归本质分析,几何代数并行

特色展台 | 回归本质分析,几何代数并行

摘要：从2024年北京卷第17题立体几何问题出发，探究本题的多种解法.在几何法的解题中，从定义出发对题目进行本质的剖析，通过建立条件和结论的关联，帮助学生找到“可操作、可迁移”的确定投影的方式;对题目进行教材类题溯源，并给出适当变式，培养学生逻辑推理、直观想象核心素养;最后，提出在立体几何模块中的教学建议. 关键词：立体几何;二面角的求法;2024年北京卷;多解探究 1 试题呈现（2024
特色展台 | 知识网络视角下的高效复习课建构

特色展台 | 知识网络视角下的高效复习课建构

《普通高中数学课程标准（2017年版）》强调，单元复习课不仅是知识的巩固，更是数学核心素养的提升过程.教师应通过系统化的知识梳理、重点难点突破、综合能力培养以及个性化辅导，帮助学生构建完整的知识体系，提升数学思维能力，为后续学习奠定坚实基础＼[1＼].“空间直线与平面”是沪教版必修第三册第10章的内容，通过本章学习，可以帮助学生认识和理解空间点、直线、平面的位置关系，能够用数学语言表述有关平行、垂
特色展台 | 选题做到两尊重归纳总结要详实

特色展台 | 选题做到两尊重归纳总结要详实

章末复习课就是要利用一两节课把一章所学知识、技能和思想方法作系统梳理，使学生对本章所涉及的概念的理解更深刻、基本方法掌握得更扎实、常规运算更熟练、认知结构更完善.就立体几何中“空间直线与平面”这一章而言，要能熟练掌握线线、线面、面面平行与垂直的证明方法，对线线角、线面角、二面角以及距离的各种作法、求法了然于胸.如何才能做到这些看似抽象的任务呢？当然要通过具体的题目来落实，我们来看张老师的做法.
课程视点 | 探骊课本习题教学培养学生具象思维

课程视点 | 探骊课本习题教学培养学生具象思维

摘要：具象思维就是运用具象的材料和因素为达到认识目的而进行的思维活动.具象思维是先于形象思维而存在的，同时也是学生抽象思维的基础、源泉.人类思维的进化是个不断从具体到抽象、从抽象到具体，再从具体到抽象的演变过程.习题教学是数学教学的一个重要组成部分，通过解题可以促使学生巩固和深化所学知识，培养思维品质.教师可挖掘习题中的情境和结构，培养具象思维直观性和概括性；挖掘习题中的图象和图式，培养具象思维跳
课程视点 | 对一道三角函数“陈题”的解法思考

课程视点 | 对一道三角函数“陈题”的解法思考

摘要：文章对一道三角函数“陈题”的惯有解法提出了质疑，给出了修改建议，提供了两种更加直观的解答，并指出数学学习要有质疑精神，要培养思维的严谨性，要注重课本概念的深度理解．关键词：陈题；严谨性；隐含条件；数学概念严谨性是数学学科的基本特点，思维严谨是学习数学最基本的要求．在平时的解题中，我们要努力做到思维严谨，不断提升思维品质．笔者发现有一类“已知条件中给出函数y=Asin （ωx+φ）+k
课程视点 | 高中教材阅读材料的教学设计探究

课程视点 | 高中教材阅读材料的教学设计探究

摘要：高中数学教材中每个章节都编排了阅读材料，这是开拓学生视野、激发学习兴趣、培养理性精神的有效资源，教师应在教学中充分利用.本文中以苏教版高中数学必修第一册第7章章末阅读材料“欧拉”为例，谈谈如何整合阅读材料进行教学设计. 关键词：数学文化；阅读材料；欧拉《普通高中数学课程标准（2017年版）》中提出：教材应把数学文化融入到学习内容中，可以适当地介绍数学和科研成果，开拓学生的数学视野，激发
教法探索 | 溯源教材：基于关键能力培养的“圆锥曲线第三定义”复习课探究

教法探索 | 溯源教材：基于关键能力培养的“圆锥曲线第三定义”复习课探究

圆锥曲线是高考考查的重点和热点内容，对数形结合、数理思维和推理运算等能力要求高，需要有较强的转化与化归、图形识别以及语言与数式形转换等能力，在求解过程中要注意思维严密，以保证结果的完备性.近年来，以圆锥曲线第三定义为背景的高考题、模拟题频繁出现.这些题目通常以教材母题为“根”，以能力立意为“魂”，注重知识的交汇性、渗透性、探究性，展现了圆锥曲线第三定义内涵与外延的“来龙去脉”，体现了数学公式和结论
教法探索 | 基于单元整体观视角的高中概率概念教学

教法探索 | 基于单元整体观视角的高中概率概念教学

摘要：高中概率内容几经演变，已形成逻辑性强、体系化的框架内容.课程标准指出，要引导学生抓住章节的内容主线，从整体上把握课程，聚焦学生学习过程，实现学生数学核心素养的形成与发展.文章基于单元整体观视角，剖析了“条件概率”的概念，梳理其在知识体系中的地位，并给出了相应的教学设计. 关键词：单元整体观；概念教学；条件概率 1 问题提出课程标准实施的关键在教师，落地在课堂.教师要转变观念，基于整体
教法探索 | 拔尖创新人才培养视域下高中数学项目化深度教学实践

教法探索 | 拔尖创新人才培养视域下高中数学项目化深度教学实践

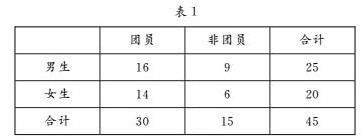
摘要：从高中育人方式改革实践出发，阐述高中数学项目化深度教学对拔尖创新人才早期发现及培养的积极作用，结合多年高中数学深度学习模式探索与实践，提出高中数学教学应“回归数学本质，落实立德树人的教育宗旨；优化教学模式，发展学生创新思维，培养学生自主学习、协作沟通能力”的深度教学理念.以此推动高中阶段学生的批判性、创造性思维能力的培养，探索拔尖创新人才的自主培养之路. 关键词：拔尖创新人才；高中数学；项
教法探索 | 条件概率与全概率公式整体教学案例

教法探索 | 条件概率与全概率公式整体教学案例

摘要：本文中重点给出了本节课七个环节的教学过程，以抽签的公平性作为情境，引出了条件概率的概念，然后再回归问题情境，教师通过问题引领，学生积极思考探索，亲身经历从特殊到一般、从直观到抽象获得条件概率概念的形成过程．最后通过一道例题巩固解决条件概率的两种方法．关键词：抽签公平；条件概率；全概率公式 “条件概率与全概率公式”是在学习了人教A版数学必修第二册第十章“概率”的基础上，于选择性必修第三册
教法探索 | 素养为本的数学概念课教学研究

教法探索 | 素养为本的数学概念课教学研究

摘要：以弧度制教学为例，在素养为本的概念教学中着力追求目标中凸显素养、问题中碰撞思维、活动中体现主体、评价中关注过程. 关键词：核心素养；概念教学；弧度制 “数学根本上是玩概念的”，概念教学是高中数学教学的核心.每个概念都是凝聚人类思维的结晶，是发展学生核心素养的宝贵素材.从素养的角度如何改进概念教学，以便让素养真正“进课堂”？除紧紧围绕传统概念教学的引入、形成、辨析等环节外，更应关注“目标中
教法探索 | 亲历概念生成，悟出“规定”之合理

教法探索 | 亲历概念生成，悟出“规定”之合理

摘要：单元起始课是大单元教学的起点，本文中以“任意角”教学设计为例，阐述起始概念课中要注意：整体教学、新知引入的必要和合理性、类比迁移、亲历生成以及体现的思想方法这几点，使核心素养培养切实落地. 关键词：任意角；起始课；合理性 1 新教材分析本节课是人教A版高一数学必修第一册5.1.1的内容，通过实际问题，树立运动变化的观点，让学生动手作图加深印象，概念建立过程中隐含的抽象、归纳、概括、类
学生学习 | “做实验”培养学生数学抽象素养

学生学习 | “做实验”培养学生数学抽象素养

《普通高中数学课程标准（2017年版2020年修订）》指出，数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养.主要包括：从数量与数量的关系、图形与图形的关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征.在平时的数学教学中，不少学生对概念认知不清晰，理解不深刻，应用解决问题容易出现偏差.数学抽象作为数学学科核心素养之一，在课堂教学中
学生学习 | 创设数学问题情境培养学生核心素养

学生学习 | 创设数学问题情境培养学生核心素养

摘要：本文中聚焦如何通过创设问题情境激发学生兴趣，引导他们主动探究数学问题.利用生活实例、问题串、故事迁移、错误范例等手段，来提升学生的数学核心素养和思维能力.教师通过创设恰当的问题情境，能让学生掌握学习的主导权，实现由“要我学”向“我要学”的积极转变，为学生的数学学习和未来发展奠定坚实基础. 关键词：高中数学；核心素养；问题情境；教学实践 “高中数学课程以学生发展为本，落实立德树人根本任务，
学生学习 | 三角形中的最值或范围问题

学生学习 | 三角形中的最值或范围问题

在高中数学知识体系中，三角形中的最值（范围）问题占据重要地位.这类问题常常紧密结合三角形的边角关系、三角函数、函数与不等式等知识，全面考查学生对多方面知识的综合运用能力与数学思维水平. 三角形中的最值（范围）问题是一类重要且具挑战性的题型.它不仅综合考查三角函数、函数与不等式等多方面知识，还对学生的数学思维与解题能力有较高要求.求解此类问题，需灵活运用各种数学方法与技巧.学生在面对此类问题时，往
学生学习 | 探析分段函数单调性

学生学习 | 探析分段函数单调性

摘要：考查分段函数单调性的试题在高考中多次出现，但学生在解决这类问题时，却经常失分.本文中基于函数单调性的定义，结合数形结合思想，利用相关图象，让学生能够深刻理解分段函数的单调性，提高解决该类问题的能力. 关键词：分段函数；单调性；数形结合 1 呈现问题已知函数f（x）=3x-1，x<1， ax，x≥1，其中a为实数，若f（x）在R上单调递增，求实数a的取值范围. 2 思考问题
学生学习 | 例析解三角形与三角函数、几何图形及平面向量结合的三类问题

学生学习 | 例析解三角形与三角函数、几何图形及平面向量结合的三类问题

解三角形与三角函数、几何图形及平面向量结合的试题，不仅能综合考查学生对多个数学概念的理解和应用能力，还能促进他们的综合思维、问题解决能力及应用意识的发展，是培养学生数学素养的重要途径之一. 1 知识点梳理（1）两角和与差的正弦、余弦与正切公式 ①sin（α±β）=sin αcos β±cos αsin β； ②cos（α±β）=cos αcos βsin αsin β； ③tan（α±
学生学习 | 基于二项式定理，挖掘展开式类型

学生学习 | 基于二项式定理，挖掘展开式类型

摘要：二项式定理在近年高考数学试卷中经常出现，创新性强，运算量大，考查方式变化多端，命题形式多样.而全面理解并掌握二项式定理及其相应的技巧方法，是解决问题的关键与基石.本文中结合实例，就二项式定理展开式中常见的几种类型加以剖析，合理构建知识网络体系，归纳总结解题技巧与方法，指导数学学习与复习备考. 关键词：二项式定理；展开式；常数项；系数；通项公式二项式定理作为一个恒等式，是高中数学知识中比
学生学习 | 函数模型应用的“三个层次”

学生学习 | 函数模型应用的“三个层次”

摘要：函数模型应用是现实生活中比较常见的一类建模应用.基于函数模型应用的层次，从图象变化，到给定模型，深入到构建模型，层层递进，实现函数模型应用的“三个层次”.本文中结合实例合理剖析，归纳总结解题技巧与步骤，夯实函数模型应用的学习与研究. 关键词：函数；模型；图象；指数；对数在描述客观世界变化规律中，函数是源于生活又高于生活的最常见且最基本的数学模型之一.数学建模中，函数模型及其应用是其中最
学生学习 | 抽象函数不“抽象”，对比思维显身手

学生学习 | 抽象函数不“抽象”，对比思维显身手

抽象函数及其综合应用问题，一直是高考命题中的热点与基本点之一.此类问题以多选题或填空题的形式来设置与应用，考查的基础知识点丰富，数学思想方法多样.在处理抽象函数问题时，可以通过赋值法把握函数特殊点的特征，逻辑推理过程比较繁杂；而借助抽象函数的运算规则等，将相应函数模型化，构建特殊函数，让抽象函数的性质“显现”出来，解题过程更加简捷，处理起来简单方便. 1 一次函数模型一次函数模型f（x）=k
学生学习 | 抽象函数问题中的单调性应用

学生学习 | 抽象函数问题中的单调性应用

摘要：作为数学抽象与应用的一个基本类型，抽象函数及其综合应用是其中最为典型的一类基本问题.而涉及抽象函数中的基本性质问题，更是应用的关键，基于抽象函数的单调性，从一些常见的基本应用类型入手，结合实例进行剖析，归纳总结解题技巧与规律，提升学生数学思维品质，培养学生数学核心素养. 关键词：抽象函数；单调性；参数；最值；范围抽象函数是函数及其基本概念中比较特殊的一类形式，是高中数学与大学数学的一个
学生学习 | 借助向量法，妙解空间角

学生学习 | 借助向量法，妙解空间角

立体几何中的空间角，主要包括异面直线所成的角、直线和平面所成的角及平面与平面的夹角（二面角）这三种，是全面集中考查考生的空间想象能力与数学运算能力等的重要场景，历来为高考命题者青睐，是高考数学命题中的必考考点之一.而合理通过空间直角坐标系的建立，借助空间向量法的巧妙应用，化“形”为“数”，数形结合，可以有效化繁杂的逻辑推理为简便的数学运算，成为解决立体几何中的空间角问题比较常见的技巧、方法之一.
学生学习 | 切线不等式的巧妙应用

学生学习 | 切线不等式的巧妙应用

摘要：基于函数与导数的综合应用，灵活运用切线不等式，是函数综合应用的深入与提升，也是问题解决过程中的“巧技妙法”.利用切线不等式，可以有效解决函数最值、参数最值、大小比较及综合应用等问题，并合理加以综合与应用，归纳解题技巧与策略，帮助学生提升综合应用能力. 关键词：函数；导数；切线不等式；参数；最值基于函数与导数的综合应用，灵活运用切线不等式，可有效解决函数与方程中的一些综合应用问题.借助切
评价透视 | 基于课程标准探究数学抽象素养三种水平试题考查特点及教学启示

评价透视 | 基于课程标准探究数学抽象素养三种水平试题考查特点及教学启示

1 课程标准要求《普通高中数学课程标准（2017年版2020年修订）》指出数学学科核心素养中的数学抽象素养的水平划分共有三个层次，各层次有不同的特点和要求：水平一要求学生能够识别和提取数学对象的基本特征，并运用符号、公式和图形表达这些特征，具备初步的抽象能力；水平二则要求学生能够对数学问题进行抽象概括，构建数学模型并解决实际问题，强调学生的抽象和概括能力；水平三则要求学生能够在更高层次上理解和
评价透视 | 一道由三角函数翻折形成立体几何试题的命制

评价透视 | 一道由三角函数翻折形成立体几何试题的命制

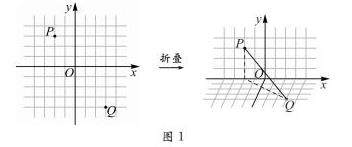
摘要：本文中把三角函数的平面问题放在空间中研究，体现了从二维到三维的思维跃进，把立体几何问题转化为平面问题来解决，体现了三维到二维的解题过程，发展了逻辑推理和数学抽象素养. 关键词：三角函数;立体几何;三角立几融合 1 展示命题（改编题）已知函数f（x）=3sin（ωx+φ）（ω>0，0<φ<π）的部分图象如图1所示，A，B分别为图象的最高点和最低点，过点A作x轴的垂线，
评价透视 | 一道立体几何与解析几何综合题目的命制

评价透视 | 一道立体几何与解析几何综合题目的命制

摘要：立体几何和解析几何是高考中的必考内容，考查学生的数学抽象、数学建模、数学运算及数据分析等核心素养.本命题小组立足几何问题设计了新定义探究，对接平面解析几何和空间立体几何两大模块，命制了一道圆锥曲线综合题目. 关键词：折叠空间距离;轨迹;椭圆 1 展示命题原创题在平面直角坐标系xOy中，有两点P（x1，y1），Q（x2，y2）.若以x轴为折痕，将直角坐标平面折叠成互相垂直的两个半平面（
评价透视 | 单元视域下的高考数学真题分析及问题设计策略

评价透视 | 单元视域下的高考数学真题分析及问题设计策略

摘要：文章以2024年新高考I卷第11题为研究对象，从单元视域角度分析试题组织、设计、呈现，并得出三点数学问题设计策略. 关键词：高考数学；单元视域；试题设计单元视域是指在教学过程中，以单元为基本单位，通过系统化的教学设计和组织，促使学生能够在特定主题或知识领域内进行深入的学习和理解.它强调教学内容的整体性和系统性，注重知识点之间的联系和逻辑结构，从而帮助学生构建完整的知识体系，提高其综合应
评价透视 | 比赛中的概率问题

评价透视 | 比赛中的概率问题

从近几年新高考的概率考查趋势来看，摒弃了浮夸的命题形式，以现实场景为创新情境，让考生把注意力集中到数学问题的本质与内涵，充分体现数学教育本身应有的务实作用与实用基础，强化了数学考查的本质，回归数学问题本源.特别，在高考数学备考与复习过程中，可以更加关注一些比赛或决策问题中的概率应用问题. 1 n局m胜制比赛问题此类比赛问题是现实生活中最常见的一类比赛赛制，其比赛的规则是：在n场比赛中，一旦比
解题天地 | 回归投影直观，妙解向量问题

解题天地 | 回归投影直观，妙解向量问题

摘要：投影作为平面向量数量积知识中的一个重要概念与创新应用，具有明显的几何意义与性质内涵．回归投影本质，合理构建对应的平面几何图形，为解决平面向量中的数量积、模、夹角以及创新定义等问题开拓一个全新的视角，指导师生的数学教学与学习以及解题研究．关键词：投影；向量；数量积；模；夹角；创新高中数学教材在平面向量的数量积部分，给出了投影与投影向量的概念，以及投影向量的计算公式等，教学时要引导学生进
解题天地 | 巧借数形结合，妙解高考真题

解题天地 | 巧借数形结合，妙解高考真题

摘要：数形结合思想是数学解题与应用中的一种常用思想方法.结合2024年高考数学真题实例，从一些问题中常见的几何内涵、代数意义、函数特征、图形本质等层面入手，合理挖掘本质与内涵，巧妙进行科学构建，依托相应的数学建模，确定与之相吻合的几何模型或图形，借助几何直观数形结合，巧妙快速分析与解决问题，有效指导复习备考. 关键词：数形结合；函数；向量；解三角形；面积我国著名数学家华罗庚说过：“数缺形时少
解题天地 | 2023年北京高考解析几何试题的解法和背景探究

解题天地 | 2023年北京高考解析几何试题的解法和背景探究

2023年高考数学北京卷第19题是一道平面解析几何解答题，其题目设计颇具匠心，旨在深入考查学生的逻辑推理能力和数学运算核心素养．题目以平易近人的姿态呈现，注重通性通法的运用，通过巧妙地设点、设线，将未知点转化为已知点，灵活运用设点代入法或设线联立来求解，充分展现了试题对解析几何基本功的扎实考查.然而，这道题目看似朴素的外表之下，实则暗含高等几何的深刻数学背景，等待着学生以敏锐的思维和深入的分析去发
解题天地 | 从通法到妙解：2023年新高考Ⅱ卷第21题的七种解法

解题天地 | 从通法到妙解：2023年新高考Ⅱ卷第21题的七种解法

1 真题呈现（2023年新高考Ⅱ卷21题）双曲线C的中心为坐标原点，左焦点为（-25，0），离心率为5. （1）求C的方程；（2）记C的左、右顶点分别为A1，A2，过点（-4，0）的直线与C的左支交于M，N两点，M在第二象限，直线MA1与NA2交于P，证明：点P在定直线上. 2 解题思路分析与思维导图 2.1 思路分析本题第（1）问比较容易，由题设条件易得双曲线的标准方程为x24
解题天地 | 一道中心三角形压轴题的深度探究

解题天地 | 一道中心三角形压轴题的深度探究

1 试题呈现例题（2024届浙江名校联盟高三联考）（多选）已知P，Q，R是椭圆C：x216+y29=1上不同的三点，△OPQ，△OPR，△ORQ的面积分别为S1，S2，S3（Si>0，i=1，2，3，O为坐标原点）.若S21+S22=S23，则（）. A.OQ⊥ORB.|OQ|2+|OR|2=25 C.S3=6D.1|OQ|2+1|OR|2为定值分析：题目以椭圆的中心三角形为背景
解题天地 | 一道解析几何高考题的解法赏析

解题天地 | 一道解析几何高考题的解法赏析

1 高考真题（2023年高考甲卷理科第20题）设抛物线C：y2=2px（p>0），直线x－2y+1=0与C交于A，B两点，且|AB|=415. （1）求p的值；（2）设C的焦点为F，M，N为C上两点，且MF5NF=0，求△MNF面积的最小值. 该题第（1）问弦长问题难度不大.第（2）问考查了三角形面积的最值问题，是圆锥曲线的常见题型，体现了高考命题的平稳性.考查了数学运算核心素养
解题天地 | 函数视角数形结合，方程层面逻辑推理

解题天地 | 函数视角数形结合，方程层面逻辑推理

摘要：函数与方程的综合应用问题是高考数学试卷中的重点与难点之一.结合一道模拟题，以函数为场景，结合含参方程的构建来确定取值范围，挖掘问题内涵，从函数本质与方程内涵这两个最基本的思维层面切入，结合不同的技巧方法来解决，指导数学教学与解题研究. 关键词：函数；方程；图象；导数含参函数与方程的综合问题，是高考数学试卷中最基础，且综合性强、难度大的一类基本常见考点，备受命题者青睐.此类综合问题，场景
解题天地 | 两边夹等价推理，“等”与“不等”妙转化

解题天地 | 两边夹等价推理，“等”与“不等”妙转化

摘要：在数学中，“相等”与“不等”是相对的，两者之间经常会根据需要加以合理化归与转化，进而得以巧妙应用.结合一道模拟题中不等式恒成立的应用场景，借助“相等”与“不等”之间的转化，合理确定对应函数的最值问题，依托“两边夹定理”来化“不等”为“相等”，进而深入应用与转化，实现问题的突破与求解. 关键词：两边夹定理；函数；不等式；取值范围；代换 “相等”与“不等”是辩证唯物主义中两个既对立又统一的整
解题天地 | 透过现象看本质，立足内涵拓思维

解题天地 | 透过现象看本质，立足内涵拓思维

在数学问题创设与综合应用场景中，“相等”与“不等”这两个不同的应用场景既是独立存在的，又是相对作用的，是辩证唯物主义中一对对立矛盾的存在，同时两者是一个统一的整体.依托数学应用场景的创新设计与综合设置，“相等”与“不等”的应用场景，看似是对立的双方，在一些具体的数学应用问题中，两者之间经常会根据实际场景及数学条件，以各种不同的形式进行合理的辩证联系，实现“相等”与“不等”之间的巧妙转化，进而加以综
解题天地 | 顺势元导遣心路，明道优术拓思域

解题天地 | 顺势元导遣心路，明道优术拓思域

作为高考中的主干知识之一的解三角形，其中相关元素或代数式的最值（或取值范围）问题的设置与考查，是命题中常见的一类综合应用问题，也是高考的热点与重点问题之一.特别是解三角形解答题，其相关元素或代数式的最值（或取值范围）的场景是多变的，或涉及角、边的最值，或涉及周长、面积的最值，或涉及综合关系式的最值等，根据不同的场景与应用条件，选取合适的技巧与方法，成为突破与解决问题的关键. 1 问题呈现问题
解题天地 | 一道含双参恒成立最值题的探究

解题天地 | 一道含双参恒成立最值题的探究

含参不等式恒成立及其相应的综合应用问题，往往以函数、方程或不等式等背景加以创设，巧妙融入含参场景，进而确定与参数有关的代数式的值或最值（或取值范围）等，成为高考数学试卷中命题的一个基本考查点.此类问题形式多样，变化多端，可以以小题（选择题或填空题）形式出现，也可以以解答题形式出现，内涵丰富，知识综合性强，常考常新.同时，此类问题的解题技巧与方法灵活多变. 1 问题呈现问题（2025届江苏省苏
解题天地 | 彰显基础突综合，探究本质提能力

解题天地 | 彰显基础突综合，探究本质提能力

解三角形及其综合应用，是高中阶段重要的基本知识点之一.立足平面向量的应用，巧妙融合平面几何、三角函数、平面向量等相关知识，是高考命题中常考常新的基本考查点.此类综合应用问题，以解答题形式设置时，场景更加丰富，内容更加充实，可以有机串联初、高中阶段相关知识点，构建不同知识模块之间的巧妙联系，合理交汇与融合，全面落实“在知识交汇点处命题”的指导精神，更加灵活巧妙地考查学生的“四基”与“四能”，备受各方
解题天地 | 函数方程转化，合理变换主元

解题天地 | 函数方程转化，合理变换主元

复杂的函数、方程或不等式等问题中一般含有常量、变量、参数等多个量.特别是基于函数或方程场景的代数式的最值（或取值范围）求解与应用问题，在实际解题时，往往需要通过变换主元或指定主元等方式，突出某个变量或几个变量的中心地位，给问题的解决提供更好的切入点与突破口，成为主元法解决问题的一种应用方式，也是解决代数式最值（或取值范围）问题的一种基本应用技巧. 1 问题呈现问题（2025届浙江省9+1高中
解题天地 | 例谈圆锥曲线中三角形面积或面积比的求解策略

解题天地 | 例谈圆锥曲线中三角形面积或面积比的求解策略

摘要：过定点的直线与圆锥曲线相交于两点，再取不共线的第三个点，便得到一个三角形.本文中研究相关三角形的面积或面积比的范围问题，通过改变定点的位置及改变曲线形式，分别探究相应的解题策略，以提升学生的逻辑推理和数学运算核心素养. 关键词：定点；直线；圆锥曲线；三角形面积；三角形面积比在圆锥曲线的高考试题中，经常考查一条动直线引发的三角形的面积或两个三角形的面积比问题.例如下面的题目.
解题天地 | 巧转化探本质拓思维

解题天地 | 巧转化探本质拓思维

摘要：所谓“化归”，从字面上看，可以理解为转化和归结的意思．化归方法，就是把待解决或未解决的问题，通过某种转化，归结到一类已经解决或者比较容易解决的问题中去，最终求得原问题解答的一种手段和方法．立体几何具有很强的抽象性，本文中通过实例分析，重点探讨了六个方面的化归方法在立体几何问题中的应用.通过优化解题方法，实现思维瓶颈的突破，提高学生解决数学问题的能力，体现数学思想方法对于培养学生的数学能力和思
解题天地 | 例谈“代数换元”的解题应用

解题天地 | 例谈“代数换元”的解题应用

近日，在学生习题训练中，发现了几例具有创新性质的关于“代数换元”的解题应用.于是，归类整理，提炼解题思维方法，旨在帮助学生拓宽解题思维视野，提高解题分析的技能技巧，提升数学运算与数学抽象方面的核心素养. 1 类型一：借助“指数、对数换元”，巧解题代数运算问题中，如果题目给出了两个等式，其中一个等式涉及指数运算，另一个等式涉及对数运算，那么我们可借助“指数换元”或者“对数换元”使得这两个等式的
解题天地 | 常考常新的正态分布试题

解题天地 | 常考常新的正态分布试题

正态分布不仅是高中数学的重要知识点，也是将来在高等数学中衡量学生数学素养的重要指标之一.新课标高考数学命题常常围绕生活实际问题中的有关正态分布的综合问题来考查，这不仅检验学生的数学能力，也反映了正态分布在现实生活和实际问题中的重要位置. 1 正态分布与新定义的综合应用例1对于一个给定的连续型随机变量X，创新定义其累积分布函数为F（x）=P（X≤x）.如图1所示，已知某系统由一个电源和三个并联
教师发展 | 利用思维导图“一点多向”的数学自主解题教学策略

教师发展 | 利用思维导图“一点多向”的数学自主解题教学策略

摘要：本文中借助思维导图辅助教学，将数学问题拆分为多个小问题，并分析各个小问题之间的关系，以发现解题的路径和规律.这种多向的思维导图能够帮助学生建立起问题解决的整体框架，同时激发学生的创造性思维和探索精神，有助于提高学生的自主学习能力，最终实现独立解决复杂的数学问题. 关键词：思维导图；一点多向；自主解题数学自主解题是培养学生创新思维和问题解决能力的重要途径之一，而思维导图作为一种有效的
教师发展 | 研究高考真题，助力高考复习

教师发展 | 研究高考真题，助力高考复习

摘要：更好更有效地进行高考复习，是每一位高三数学教师追求的根本目标.从研究高考真题视角切入，合理寻找知识共性，探索命题趋势，总结考点规律，探寻变化特点等，更加服务于高考复习的“教”与“学”，有效提升高考数学复习效率，助力高考复习. 关键词：高考真题；知识；命题；考点；变化年年岁岁花相似，岁岁年年题不同.研究一年一度的高考数学真题以及以往各年的高考数学真题，是每位高中数学教师，特别是高
教师发展 | 基于任务群的高中数学教学实践与思考

教师发展 | 基于任务群的高中数学教学实践与思考

摘要：在新课改不断深化的进程中，利用任务群进行教学是一线教师探讨的新话题，本文中以高中数学教学实践为探讨载体，基于任务驱动的视角，从“自主任务、导学任务、拓展任务”三个角度进行剖析，重点探讨高中数学问题本质规律的发现、解题策略的形成和学生学科核心素养的提升，以期实现教学相长的目的. 关键词：高中数学；教学实践；任务群；素养新课程标准实施以来，提升学生学科核心素养已经成为课堂教学关注的焦点
教师发展 | 高中数学新课程中的三角函数与三角关系

教师发展 | 高中数学新课程中的三角函数与三角关系

摘要：随着教学的改革，高中数学新课程内容有较大变化，需要教师在整体上进行教学设计并提高教学质量.“三角函数与三角关系”这部分内容在高中数学新课程中的教学编排上有一些变化，对这些关系进行分析可以提高学生思维能力和判断能力.本文中结合高中数学新课程对三角函数与三角关系的正确应用进行了分析，并提出了教学建议. 关键词：高中数学；新课程；三角函数与三角关系三角函数是高中数学新课程中的重难点内容，
教师发展 | 构建课堂学习共同体，引导学生深度学习

教师发展 | 构建课堂学习共同体，引导学生深度学习

摘要：协同构建课堂学习共同体，是教学与学习环节中一个非常重要的环节.借助创新情境的创设，展现思维过程，从团体协作的交流及学习反思的引导等方面入手，合理引导学生进行深度学习，提升学习的质量与效应，引领并指导数学教学与学习. 关键词：学习共同体；深度学习；教师；学生深度学习作为一种有意义的学习模式，是学生自身源于本身动机的对有价值的学习内容展开的一系列理解性、阶梯式的学习，是一个完整的、
教师发展 | 高中数学结构不良试题特征分析及应对策略

教师发展 | 高中数学结构不良试题特征分析及应对策略

摘要：高中数学结构不良试题是培养学生知识和能力水平的重要载体.文章从考查意义、特征分析及应对策略三个层面对试题进行分析，有助于优化高中数学教学. 关键词：高中数学；结构不良试题；应对策略高中数学中结构不良问题的内涵在于它们以模糊、条件不完整或不明确的形式呈现，使得学生在解决这些问题时，需要具备更强的理解能力、逻辑推理能力及创造性的思维方式. 1 结构不良试题考查意义 1.1 落实
教师发展 | 基于立体几何的深度理解构建高品质课堂

教师发展 | 基于立体几何的深度理解构建高品质课堂

摘要：本文中以直线与平面所成的角的求法为例，以“面面垂直的性质”作为课堂灵魂，利用一题多解的形式培养学生对直接法、转移法求解线面角的运用能力；最后，对构建高品质课堂的策略进行了分析. 关键词：高品质课堂；深度理解；立体几何；直观想象 1 构建高品质教学课堂之价值高品质课堂是指教师在传统教学模式基础上，以学生的认知发展为培养目标，以高品质、高质量、高成效为原则，构建的有针对性的课堂.
教师发展 | 巧设问题，助推深度学习

教师发展 | 巧设问题，助推深度学习

摘要：问题是数学的心脏，问题能引导学生思考，推动其探究，促使其实践，从而发展思维. 巧设问题驱动，从而引发学生展开真思考、真探究、真表达.本文中从一个核心问题出发，多维度深度探究，从而促进深度学习的发生，发展学生的高阶思维，让学生的核心素养得以生成. 关键词：问题驱动；深度学习；高阶思维问题设计是思维触发的基础，问题探究是思维进阶的核心，问题迁移是思维升华的关键，课堂文化和思维评价
教师发展 | 构造对偶式，妙解三角题

教师发展 | 构造对偶式，妙解三角题

摘要：在解决一些相关的三角函数综合应用问题时，合理挖掘题设内涵与问题实质，借助相应三角函数中对应类型的“对偶式”的构造与应用，可以使得问题解决更加优美简洁.结合实例，就三角函数问题中一些常见“对偶式”的构造方法与应用技巧加以剖析，展示优美解法，开拓数学思维. 关键词：三角函数；对偶式；正弦；余弦；应用合理构造对偶式，巧妙解题，是解答一些函数或方程、不等式等相关问题时的一种巧妙的解题技巧与

2024年上海高考第21题的探究
回归本质分析,几何代数并行
知识网络视角下的高效复习课建构
选题做到两尊重归纳总结要详实
探骊课本习题教学培养学生具象思维
对一道三角函数“陈题”的解法思考
高中教材阅读材料的教学设计探究
溯源教材：基于关键能力培养的“圆锥曲线第三定义”复习课探究
基于单元整体观视角的高中概率概念教学
拔尖创新人才培养视域下高中数学项目化深度教学实践
条件概率与全概率公式整体教学案例
素养为本的数学概念课教学研究
亲历概念生成，悟出“规定”之合理
“做实验”培养学生数学抽象素养
创设数学问题情境培养学生核心素养
三角形中的最值或范围问题
探析分段函数单调性
例析解三角形与三角函数、几何图形及平面向量结合的三类问题
基于二项式定理，挖掘展开式类型
函数模型应用的“三个层次”
抽象函数不“抽象”，对比思维显身手
抽象函数问题中的单调性应用
借助向量法，妙解空间角
切线不等式的巧妙应用
基于课程标准探究数学抽象素养三种水平试题考查特点及教学启示
一道由三角函数翻折形成立体几何试题的命制
一道立体几何与解析几何综合题目的命制
单元视域下的高考数学真题分析及问题设计策略
比赛中的概率问题
回归投影直观，妙解向量问题
巧借数形结合，妙解高考真题
2023年北京高考解析几何试题的解法和背景探究
从通法到妙解：2023年新高考Ⅱ卷第21题的七种解法
一道中心三角形压轴题的深度探究
一道解析几何高考题的解法赏析
函数视角数形结合，方程层面逻辑推理
两边夹等价推理，“等”与“不等”妙转化
透过现象看本质，立足内涵拓思维
顺势元导遣心路，明道优术拓思域
一道含双参恒成立最值题的探究
彰显基础突综合，探究本质提能力
函数方程转化，合理变换主元
例谈圆锥曲线中三角形面积或面积比的求解策略
巧转化探本质拓思维
例谈“代数换元”的解题应用
常考常新的正态分布试题
利用思维导图“一点多向”的数学自主解题教学策略
研究高考真题，助力高考复习
基于任务群的高中数学教学实践与思考
高中数学新课程中的三角函数与三角关系
构建课堂学习共同体，引导学生深度学习
高中数学结构不良试题特征分析及应对策略
基于立体几何的深度理解构建高品质课堂
巧设问题，助推深度学习
构造对偶式，妙解三角题

过往期刊

更多

中学数学·高中版
2025年04期
中学数学·高中版
2025年03期
中学数学·高中版
2025年02期
中学数学·高中版
2025年01期

猜你喜欢

兴趣阅读·少年诗刊
2025年04期
学习方法报·读写拍档新高考版
2025年50期
学习方法报·读写拍档高中版
2025年50期
学习方法报·政治新高考版新教材
2025年48期
学习方法报·历史新教材高一
2025年48期
学习方法报·政治新教材高二
2025年48期
学习方法报·写作（高二）
2025年48期
学习方法报·历史新高考版新教材
2025年48期

Copyright © 2017 龙源数字传媒集团京ICP备060024号
Dragonsource.com Inc. All Rights Reserved
IP:18.219.23.38

上海外国语大学电子阅览室

首页
全部分类
排行榜
客户端下载

登录
个人中心我的收藏退出登录
简体 / 繁体

上海外国语大学电子阅览室

忘记密码新用户

新用户注册

已有账户

注册成功

修改电子邮件