全部分类/
教育教学/
中学数学·高中版

中学数学·高中版

2025年02期

扫码免费借阅

目录

快速导航

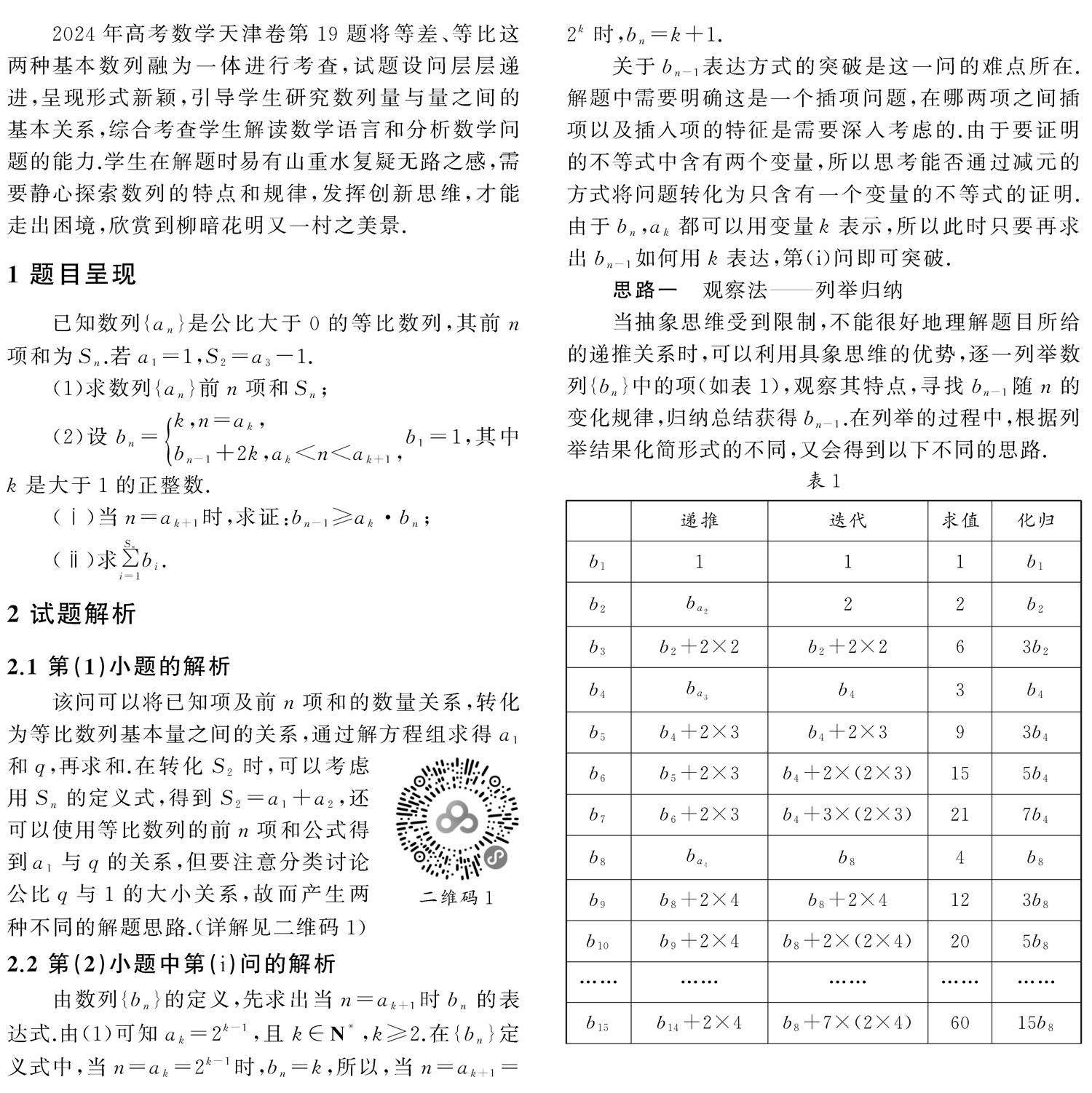
特色展台 | 山重水复探试题奥秘柳暗花明显创新思维

特色展台 | 山重水复探试题奥秘柳暗花明显创新思维

摘要：2024年高考数学天津卷第19题是一道数列大题，以等比数列为背景，通过递推关系将等差数列融入其中，考查数列基本概念和公式，涉及与数列有关的数列通项、不等量关系证明、数列求和等问题，综合考查学生解读数学语言和分析数学问题的能力. 关键词：数列求和；不等式证明；数学核心素养；创新思维 2024年高考数学天津卷第19题将等差、等比这两种基本数列融为一体进行考查，试题设问层层递进，呈现形式新颖，
特色展台 | 一石激起千层浪吹尽黄沙始见金

特色展台 | 一石激起千层浪吹尽黄沙始见金

摘要：2024年全国甲卷理科第21题的第（2）问是有关含参不等式恒成立求参数取值范围的问题，是一道涉及导数应用的压轴题.本文中重点对第（2）问进行探究，首先通过思维导图分析解决该问题的分类讨论、端点效应、参变分离、切线放缩、对数平均不等式等思路，然后给出对应的7种具体解法，接下来给出试题的溯源及拓展，最后进行反思总结. 关键词：导数压轴题；含参不等式恒成立；思维导图；解题分析课题信息：四川省
特色展台 | 基于教材的拓展课：一道例题的引申及应用

特色展台 | 基于教材的拓展课：一道例题的引申及应用

1 教学分析本节课的教学目标：（1）借助教材例题中的几何模型引申出“三余弦定理”及求二面角的面积射影公式；（2）引导学生观察教材例题模型，探索过一点的三条线段构成三面角之间的关系，进而发现“三余弦定理”和求二面角的面积射影公式；（3）通过对例题的引申、发散，培养学生利用现有资源发现问题、提出问题和解决问题的能力. 本节课的教学重难点：重点：探究得出“三余弦定理”、最小角定理及
特色展台 | 在例习题教学中提升学生思维品质

特色展台 | 在例习题教学中提升学生思维品质

教材是教学之本，充分利用教材例题、习题资源，挖掘例题、习题潜在的教学价值，在这一过程中，学生的分析问题、提出问题和解决问题能力等思维品质得到提升，对提升教师理解和驾驭教材的能力也很有帮助，特别是年轻教师. 王定老师从教第5年，教过一轮高中，从高一刚进入高二.王老师从教材中一道例题入手，通过从不同角度引导学生观察、分析、思考、研讨、归纳总结，提出“三余弦定理”、求二面角的面积射影法及最小角定理.这
课程视点 | 多元融合提升高中数学教学质量的策略探究

课程视点 | 多元融合提升高中数学教学质量的策略探究

摘要：立足多元融合提升高中数学教学质量的重要价值，本文中通过案例分析，提出了“强调学生主体地位，应用多样化的教学方式”“重视实际应用，创设合适的教学情境”“强化资源整合和学科融合，提升学生跨学科综合素养”“注重教学实践，激发学生学习兴趣”提升高中数学教学质量的几个策略. 关键词：新课改；多元融合；高中数学；教学实践 1 多元融合提升高中数学教学质量的价值指向 1.1 顺应新课改要求新课程
课程视点 | 新课程背景下基于数学史的数学文化在高中数学课堂的应用研究

课程视点 | 新课程背景下基于数学史的数学文化在高中数学课堂的应用研究

摘要：新课程背景下探究数学史在高中数学课堂中的应用实践意义明显.文章从加工高中数学教材、设计融入数学史的习题、创新与课堂有关的数学史活动设计三个层面分析了课堂中融入数学史的方法. 关键词：新课程背景；高中数学；数学文化；应用策略在新课程背景下，强调素养导向的教学目标，基于数学史的数学文化在高中数学课堂的应用显得尤为必要.通过数学史，学生不仅能够理解数学概念的形成过程和发展脉络，还能体会到数学
课程视点 | “阅读与思考”：依托数学文化，学习画法几何

课程视点 | “阅读与思考”：依托数学文化，学习画法几何

摘要：数学文化的渗透与融入经常以“阅读与思考”等栏目的形式出现在高中数学教材中，教学中要合理引导学生进行课外阅读与拓展提升.结合画法几何的起源与应用所对应的“阅读与思考”栏目，深入研究相应的数学文化，通过画法几何与空间直观图等的应用，渗透画法几何的思维，实现数学文化的融合与应用，指导数学教学与复习备考. 关键词：画法几何；直观图；空间几何体；数学文化数学文化的创新设置与巧妙融合，是新高考数学
教法探索 | 以问题为驱动聚焦核心素养下课堂“真学习”探究

教法探索 | 以问题为驱动聚焦核心素养下课堂“真学习”探究

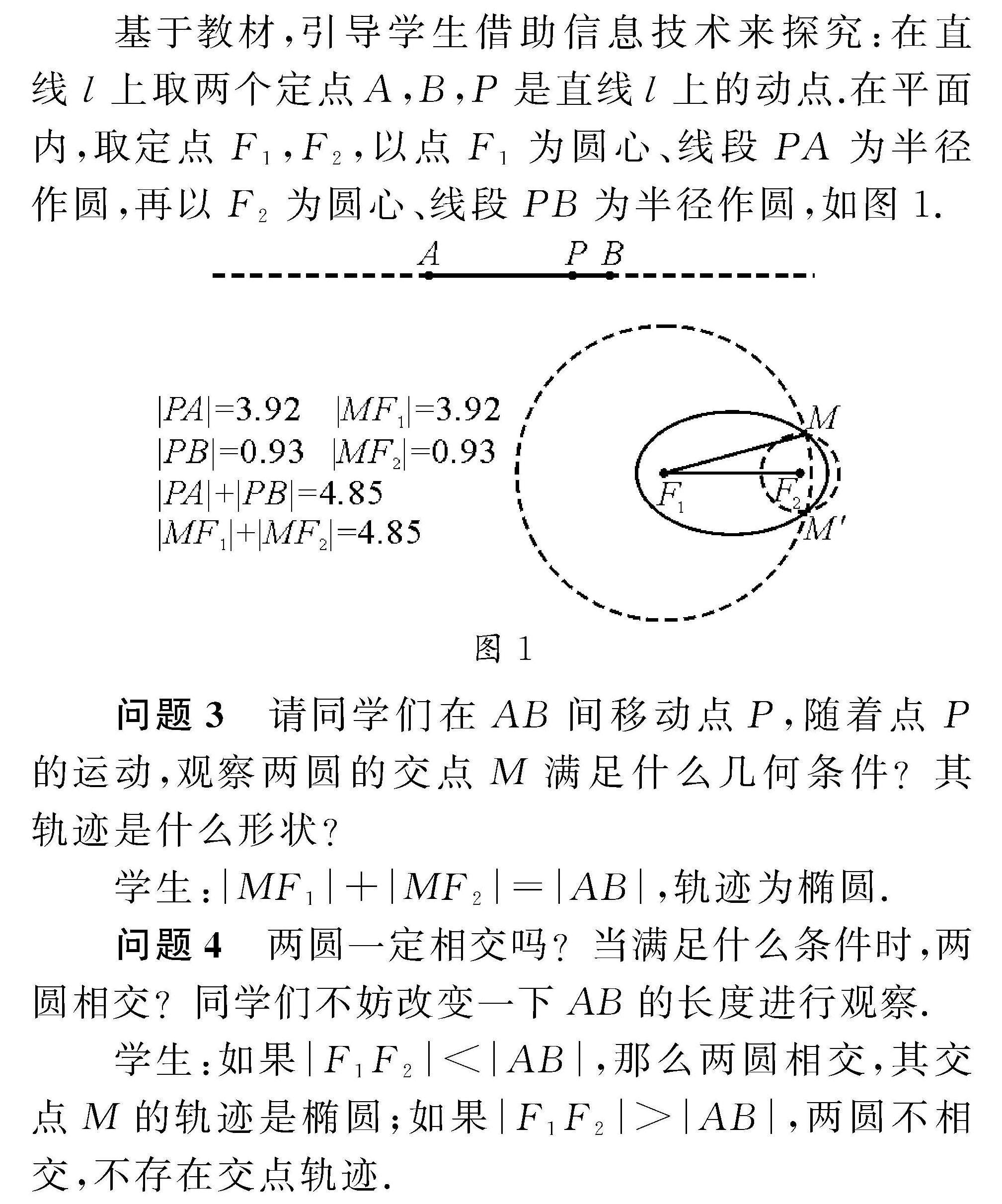
摘要：长期以来，专家学者提出教学理论与一线教师的教学实践在教学活动的基本问题上，常常各有所偏.本文中探索“问题”驱动下课堂中的真学习，该“真学习”是通过设置各种问题为抓手，不仅能调动学生的学习兴趣，而且能激发学生多感官的学习激情，更能促进学生透过现象发现其背后的规律，实现课堂中“真学习”的发生、发展. 关键词：高中数学;真学习;问题驱动;核心素养数学学科核心素养的本质是描述一个人经过数学教育
教法探索 | U型探究思维下双曲线单元教学设计

教法探索 | U型探究思维下双曲线单元教学设计

摘要：双曲线这节在单元教学的理念下，以比较椭圆和双曲线在定义、标准方程、图形特征和a，b，c的关系上的异同为知识层面的明线，以类比法、坐标法、轨迹法和数形结合法等研究方法和猜想、验证、证明等研究思路为能力与素养层面的暗线，以经验的生长与改造、方法的类比与验证、问题的迁移与反思为内在逻辑线设计一系列自然而然的学习活动.这种思维探究模式恰似一个“U型”，培养学生渴求知识的感觉，使学生获得“如何思考”的
教法探索 | 从“一题多解”到“一题多变”

教法探索 | 从“一题多解”到“一题多变”

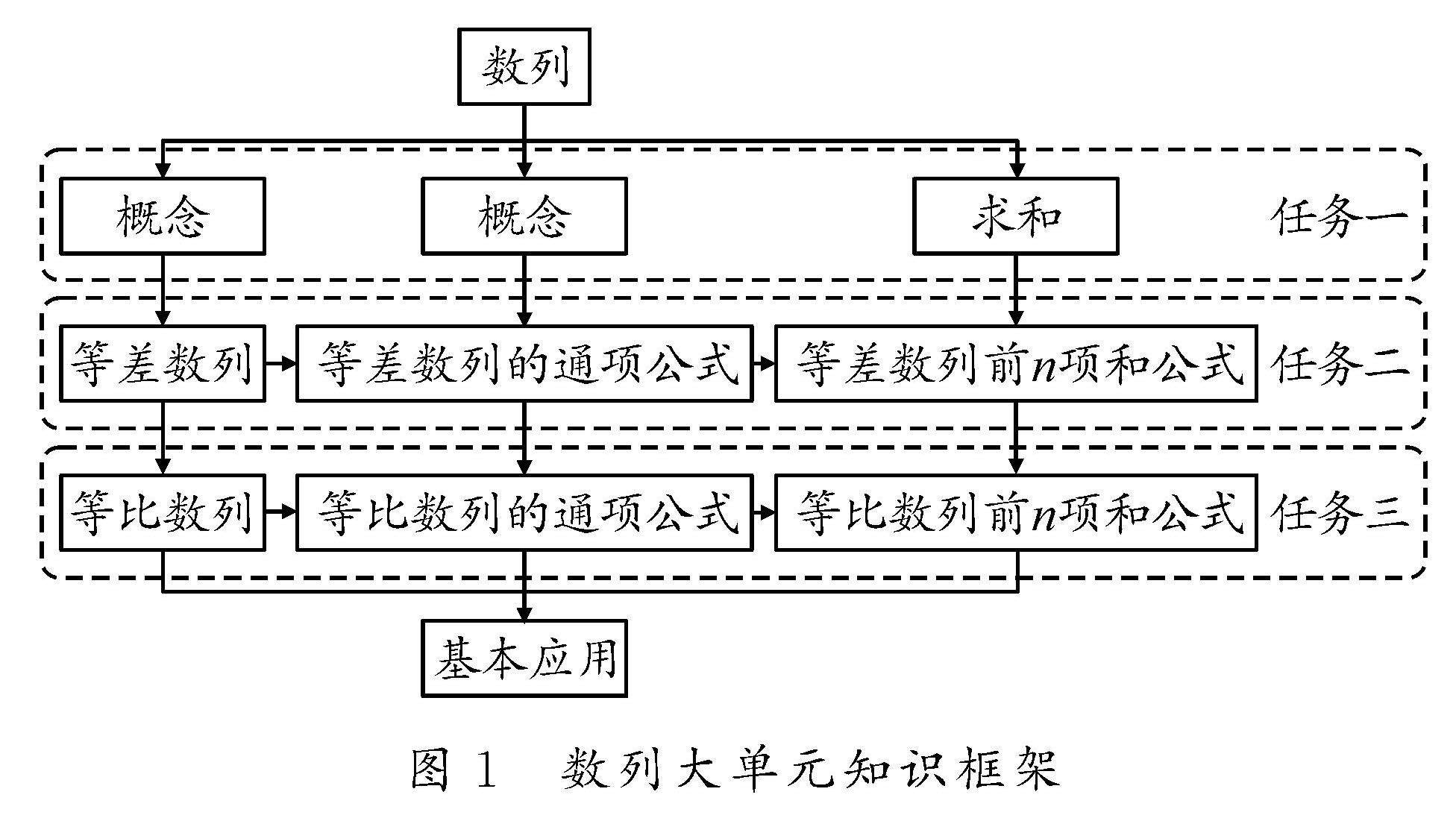
项目信息：福建省中青年教师教育科研项目（基础教育研究专项）“核心素养视域下高中数学拓展类校本课程建设研究”，项目编号为JSZJ23122.福建教育学院资助. 解三角形是高考数学必考的一个知识点，侧重考查正弦定理、余弦定理与面积公式在解题中的灵活运用.由于此类问题通常以图形为载体进行设计，且涉及到的具体运算往往较多，所以有利于较好地培养学生在直观想象与数学运算方面的核心素养. 好题采撷在△A
教法探索 | 基于数学核心素养的高中数学大单元教学设计的研究

教法探索 | 基于数学核心素养的高中数学大单元教学设计的研究

摘要：基于数学核心素养的培养，教师对课堂教学模式进行创新，运用大单元的教学设计模式来突出学科知识的特点，强化学生的思考能力以及实践应用能力.本文中分析如何对高中数学知识体系进行大单元教学设计，落实新课标教学要求，培养学生的学科核心素养. 关键词：高中数学；学科核心素养；大单元教学设计课题信息：无锡市教育科学“十四五”规划课题“核心素养导向的高中数学大单元教学设计研究”，课题编号为B/C-b/
教法探索 | 项目式教学的设计与实施

教法探索 | 项目式教学的设计与实施

课题信息：江苏省中小学教学研究第十五期课题“核心素养视域下的‘项目式学习+跨学科’融创课程校本化管理的实践研究”，课题编号为2023JY15-GL-L171. 1 实施背景本课程设计聚焦于“用样本估计总体”这一教材内容，结合本校的实际情况，将数学与社会学学科融合，利用“双环互动”项目式学习模式，培养学生的核心素养，特别是数据分析与跨学科综合应用能力. 2 教学目标本课程设计通过项目式学
教法探索 | 核心素养导向的高中数学大单元教学策略研究

教法探索 | 核心素养导向的高中数学大单元教学策略研究

摘要：在核心素养导向下探究高中数学大单元教学策略有利于指导教学.文章从划分单元内容、分析教学要素、制定教学目标、准备预习资料、细化教学设计、评价教学效果六个方面提出策略，为教学提供借鉴. 关键词：核心素养；高中数学；教学策略课题信息：无锡市教育科学“十四五”规划课题“核心素养导向的高中数学大单元教学设计研究”，课题编号为B/C-b/2021/01. 研究核心素养导向的高中数学大单元教学策略
教法探索 | 突出概念性质，指向核心素养

教法探索 | 突出概念性质，指向核心素养

摘要：数学学科核心素养的指向必须扎根于数学课堂教学与学习，基于数学知识的学习来实现核心素养的培养与提升，这已经成为数学教学与学习的一个常态.本文中通过以“函数的概念与性质”单元教学设计为例，立足单元教学根本，突出函数的基本概念与基本性质，指向核心素养的培养与提升，指导数学教学与学习. 关键词：概念；性质；核心素养；函数；单元教学设计课题信息：甘肃省教育科学“十四五”规划2023年度专项课题“
教法探索 | 基于大单元复习课的项目化学习的教学实践

教法探索 | 基于大单元复习课的项目化学习的教学实践

摘要：“齐次”从字面上解释是“次数相同”的意思，“齐次化”则是对方程的一种处理方法，使得方程中各项参数的次数相同.“齐次化方法”其本质是应用了更加广泛的曲线方程，该解法能够极大地简化相关计算过程，是一种很好的解题方法.熟练掌握“齐次化方法”，学生在考场上能够应对自如，手到擒来. 关键词：齐次化方法；大单元复习课；斜率；定值大单元复习课注重课程目标与教学内容之间的整合联系，体现整体化的教学思维
教法探索 | 例谈五环节模式在高中数学教学中的实践

教法探索 | 例谈五环节模式在高中数学教学中的实践

摘要：相较于传统的被动式教学课堂，高效课堂五环节教学模式具有显著的特点.这种教学模式强调学生的主观能动性，以学生为教学的核心，通过五个主要环节——目标引入、自主合作学习、精讲点拨、有效训练和评教评学，来提高高中生的数学学科核心素质.本文中以“基本不等式”为例分析高效课堂五环节模式在高中数学教学中的实践，并归纳了要注意的事项. 关键词：高中数学；高效课堂；五环节项目信息：江西省学位与研究生教育
教法探索 | 内容自然学得自然教得自然

教法探索 | 内容自然学得自然教得自然

摘要：数学是自然的，数学概念的产生与发展也具有自然性.基于章建跃博士提出的理解数学、理解学生、理解教学的理论，本文中以“二面角的概念”教学为例，进行了体现概念教学自然性的教学设计与实践，试图探索一种内容自然、学得自然、教得自然的概念课教学模式. 关键词：概念;教学;自然课题信息：2021年度重庆市教学科学“十四五”立项一般课题“基于深度学习的高中新教材概念教学实践研究”，课题批准号为20
教法探索 | 基于多元表征理论的高中数学教学案例分析

教法探索 | 基于多元表征理论的高中数学教学案例分析

摘要：数学多元表征是指同一数学学习对象的多种表征形式.在高中数学学习中，单一的文字语言已经不能满足定义阐述的需要，因此，应用数学多元表征理论指导教学是提升教学质量的必经之路.本文中深入剖析一节融入了数学多元表征理论的“函数的单调性”教学案例，体会数学多元表征理论在教学中的灵活应用. 关键词：数学多元表征；单调性；教学过程项目信息：哈尔滨师范大学高等教育教学改革研究项目“数学与应用数学专业师范
教法探索 | 关于“椭圆的几何性质”研究课教学设计的再思考

教法探索 | 关于“椭圆的几何性质”研究课教学设计的再思考

摘要：椭圆是高中解析几何中最重要的圆锥曲线.椭圆的学习为双曲线和抛物线的学习起到示范作用，同时椭圆也是学生面临的第一条用解析方法研究的圆锥曲线，因此教师在教学上需要有思考，有创新. 关键词：学生视角；教学设计教学研究需要突破常规，在传统的基础上进行新尝试，利用这些新尝试为教学添加新的选项.“椭圆的几何性质”是高中阶段十分重要的一节，过往很多教师都就此做过研究课.笔者也曾在2018年开设了一节
教法探索 | 深度学习铸就活力课堂

教法探索 | 深度学习铸就活力课堂

引导学生深度学习，铸就活力课堂，是落实新课标指向的重要路径.深度学习是相对于浅层次学习而言的.所谓数学深度学习，是指学生在教师的引导下，围绕具有一定难度且具有一定挑战性的数学主题展开学习和深层次的探究，在整个过程中学生都能全身投入并体验成功.“活力”是活力课堂的落脚点，充满活力的课堂往往能引发笑声，并能激发探究的欲望，探究过程中，必然会有互相交流的讨论声，当探究成功分享喜悦时，必然会引发阵阵掌声.
学生学习 | 借空间动态问题培养直观想象能力

学生学习 | 借空间动态问题培养直观想象能力

近期，以“关注学教评，迎接新挑战”为主题的教学研讨活动在某兄弟学校举办，笔者受邀面向该校高三学生开设了一节微专题课.考虑到一轮复习接近尾声，学生已经掌握了立体几何的基本知识，于是就以“立体几何中的动态问题”为课题，编制学案并提前发给学生预习.下面将这节课的教学过程整理如下，并结合课例谈谈直观想象能力的培养问题. 1 教学分析本节课研究立体几何中的动态问题，包括动点形成的轨迹、运动过程中的位置
学生学习 | 剖析试题情境培养理性思维

学生学习 | 剖析试题情境培养理性思维

摘要：文章以两道质检试题为例，从不同角度剖析试题情境，提出了深度剖析情境，发展学生思维的启示. 关键词：试题情境；解题思路；发展思维《中国高考评价体系说明》指出，在试题命制层面，进一步强调情境化设计［1］.试题情境是实现考查内容和考查要求的载体，学生解决问题时，需要在理解与提取、分析与推理、归纳与表达的基础上，寻求解决问题的途径.下面，笔者以两道质检试题为例，谈谈引导学生合理剖析试题情境，联
学生学习 | 设置挑战性学习任务，助推数学思维进阶

学生学习 | 设置挑战性学习任务，助推数学思维进阶

摘要：挑战性学习任务能够通过探索式学习引导学生发展思维，建构理性的知识逻辑链，促进知识、技能、思想的共融共生，从而实现螺旋式上升，形成高品质的数学核心素养.本文中以高中数学课本中的一道习题为切入点重构反思，探索以一题多变设计挑战性任务，实现思维进阶. 关键词：挑战性任务；高中数学；一题多变；思维进阶高中数学的挑战性学习任务是指在教学中设计的一种具有挑战性、旨在促进学生深度学习和思
学生学习 | 转化与化归思想在高中数学试题中的应用特征分析及教学启示

学生学习 | 转化与化归思想在高中数学试题中的应用特征分析及教学启示

摘要：转化与化归思想是高中数学试题考查的重要思想之一，文章以一道典型例题为研究对象，分析试题是如何体现转化与化归思想的考查的，结合教学实际，总结出转化与化归思想在高中数学试题中的应用特征，并提出教学策略. 关键词：高中数学；转化与划归思想；教学策略转化与化归思想是高中数学中重要的数学思想方法，是指通过将复杂问题转化为已知或更简单的形式，或者将问题归结为已掌握的数学模型或方法进行解决的过程［1
学生学习 | 圆锥曲线中几种简化运算的处理方法

学生学习 | 圆锥曲线中几种简化运算的处理方法

摘要：圆锥曲线问题是高考的热点问题，也是难点问题，对学生运算能力要求较高，本文中主要例谈了圆锥曲线问题的几种简化运算的处理方法. 关键词：圆锥曲线；简化运算圆锥曲线问题是高考的热点问题，也是难点问题，对学生的逻辑推理和数学运算两大核心素养有着较高要求.如何简化圆锥曲线问题的运算呢？笔者以近几年高考题为例，谈谈一些处理策略. 1 利用“曲线与方程思想”减计算方程Ax2+By2+Cxy+D
学生学习 | 巧用“角”，解决双曲线离心率的问题

学生学习 | 巧用“角”，解决双曲线离心率的问题

摘要：在近几年的高考、模拟考试中有不少涉及双曲线离心率的问题.学生在解决此类问题时，经常束手无策，或者由于运算量大而中途放弃.本文中主要介绍求解双曲线的离心率问题时，考虑双曲线的对称性，利用渐近线的斜率、倾斜角，结合条件分析出a，b之间的关系，再计算离心率，突破重难点. 关键词：双曲线;渐近线;斜率;离心率例1 （2023湛江二模）（多选）已知双曲线C：y2a2－x2b2=1（a>0
学生学习 | 导数在解三角函数问题中的运用

学生学习 | 导数在解三角函数问题中的运用

摘要：导数为研究函数提供了新的方向，因此导数与三角函数相结合的问题也成为了高考的一类热点问题.导数与三角函数的结合，是在函数背景下考查三角函数问题，主要涉及求导公式、导数的几何意义、解三角形、三角恒等变换等基础知识，且在选择题、填空题以及解答题中均有较大的几率出现.本文中主要通过相应的例题帮助学生分析常考题型的解题要领，以便提升正确率. 关键词：导数；三角函数；解题技巧导数是中学数学的重要内
学生学习 | 基于保持特殊性质，探寻动点轨迹

学生学习 | 基于保持特殊性质，探寻动点轨迹

摘要：立体几何中的动点轨迹及其应用问题，是高考数学命题中的重点与难点之一.在立体空间的应用场景下，基于动点保持所对应元素性质如平行关系、垂直关系、等距关系及等角关系等的轨迹及其应用问题，结合实例就一些常见的基本性质类型加以剖析应用，归纳总结解题技巧与策略，指导数学教学与复习备考. 关键词：立体几何；动点；轨迹；平行；垂直立体几何中的动点轨迹问题，是以空间图形为基本素材，借助符合一定特殊条件的
学生学习 | 追根溯源链接高考，开拓思维一题多解

学生学习 | 追根溯源链接高考，开拓思维一题多解

摘要：有关曲线的对称中心与对称轴是函数图象中对称性的一个重要方面，也是数与形巧妙融合的一个重要场景.结合一道高考模拟题中有关函数所对应曲线的对称中心的确定，展开联想，追根溯源，链接高考，开拓思维，一题多解，借此归纳总结解决此类问题的基本技巧方法，指导数学教学与复习备考. 关键词：函数；曲线；对称中心；奇函数；定义在高中数学中，研究函数的基本性质时一般要研究函数图象的对称性，而这就离不开相关函
学生学习 | 巧借积化和差公式，妙破解三角形问题

学生学习 | 巧借积化和差公式，妙破解三角形问题

摘要：三角函数中的积化和差公式，是两角和与差公式的一个深入应用与变式拓展，也是解决三角函数问题时常用的一组特殊公式.在处理解三角形的综合应用问题时，涉及三角形内角的三角函数值，经常借助积化和差及相关公式加以转化与应用，巧妙破解相应的的解三角形问题.结合典型实例剖析，总结归纳解题技巧与规律方法，引领并指导数学教学与解题应用. 关键词：积化和差；解三角形；求值；内角；最值三角函数中的积化和差公式
学生学习 | 一道数量积取值范围题的探究

学生学习 | 一道数量积取值范围题的探究

摘要：涉及平面向量数量积的取值范围（或最值）的求解以及创新应用问题，是高考命题中比较常见的一类基本考查类型.本文中结合一道特殊场景下的数量积的取值范围的求解，立足“数”与“形”等不同数学思维视角加以巧妙切入与应用，剖析不同的解题技巧方法，合理深入拓展变式与研究，有效提升数学思维与能力的高度与维度，有效指导解题研究与复习备考. 关键词：平面向量；数量积；取值范围；坐标；几何平面向量的数量积，作
评价透视 | “双新”背景下高中数学分层作业设计及评价研究

评价透视 | “双新”背景下高中数学分层作业设计及评价研究

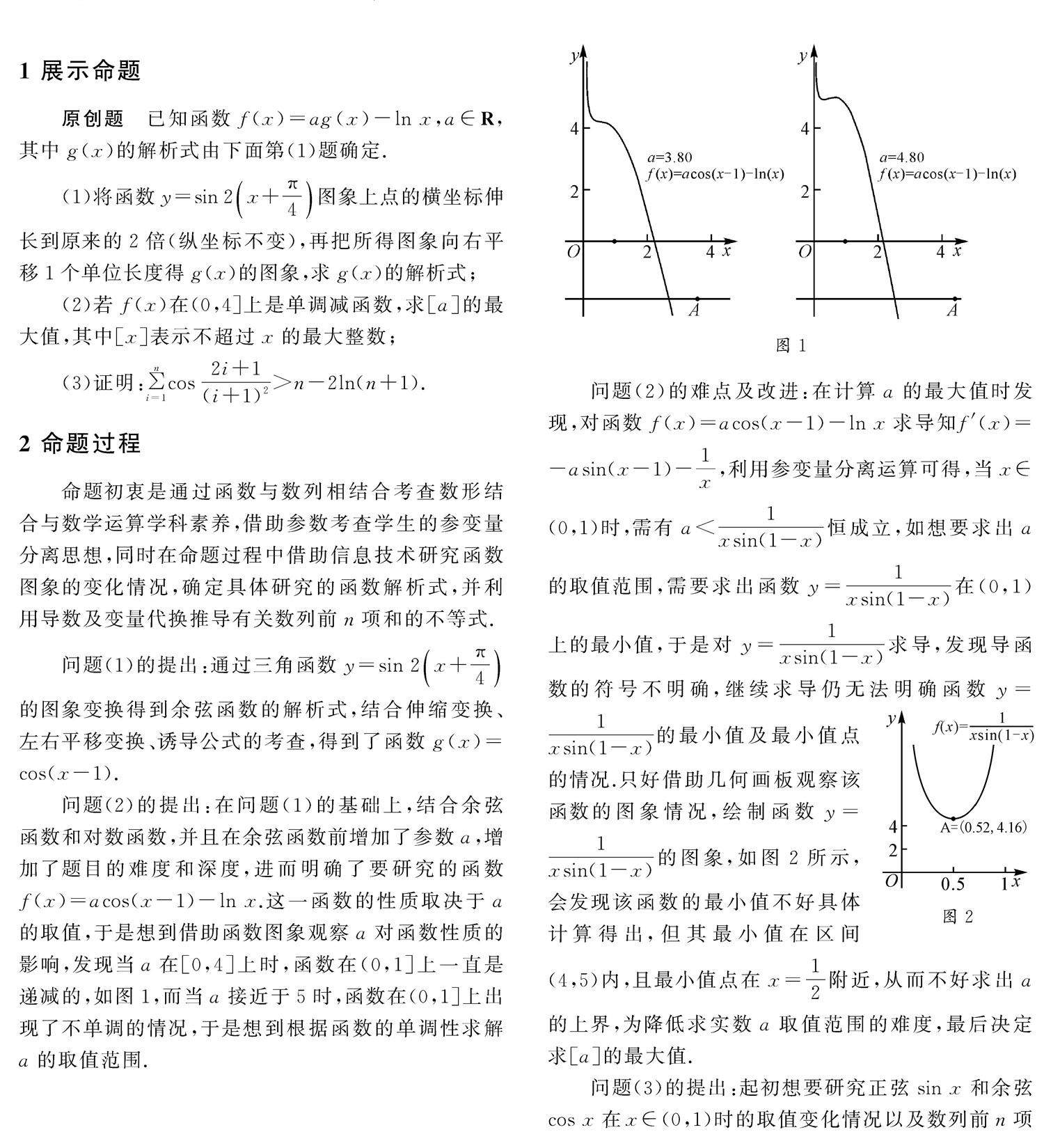
摘要：高中数学分层作业设计及评价的研究旨在探讨“双新”背景下高中数学分层作业设计及评价策略，力求通过科学合理的作业分层，满足不同学习水平学生的需求，促进全体学生的个性化发展与全面提升.通过理论分析与教学实践相结合，提出了基于学生能力差异的分层作业设计理念，构建了多元化评价体系，并结合具体案例，展示了分层作业设计在高中数学教学中的有效应用，为“双新”改革背景下的数学教学提供了实践参考与理论支持.
评价透视 | 着眼高考热点问题聚焦教材难点融合

评价透视 | 着眼高考热点问题聚焦教材难点融合

摘要：本文中通过结合高考中的函数与数列两类热点命制了一道解答题，旨在考查学生数形结合和数学运算素养，提升学生对知识的理解和综合运用能力. 关键词：三角函数；对数函数；数列；不等式 1 展示命题原创题已知函数f（x）=ag（x）－ln x，a∈R，其中g（x）的解析式由下面第（1）题确定. （1）将函数y=sin 2x+π4图象上点的横坐标伸长到原来的2倍（纵坐标不变），再把所得图象向
评价透视 | 基于数学问题情境命制的一道概率题目

评价透视 | 基于数学问题情境命制的一道概率题目

摘要：《中国高考评价体系说明》提出要发挥问题情境在考查学生必备知识、关键能力、学科素养和核心价值四个层面的重要价值.情境化问题是学生核心素养形成、发展和表现的载体.以数学情境为背景，记录命制一道概率试题的过程. 关键词：数学情境；二项分布《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课标》）强调，数学学科核心素养的水平需要在特定情境中进行考查.问题情境是考查数学学科核心素
评价透视 | 巧借韦达定理破解斜率之商

评价透视 | 巧借韦达定理破解斜率之商

摘要：直线与圆锥曲线问题是解析几何中的重要内容，韦达定理是解决这类问题的关键工具.本文中将通过一道原创题目的分析和详细讲解，帮助读者更好地理解和应用韦达定理. 关键词：圆锥曲线；直线；韦达定理 1 题目呈现原创题椭圆C：x2a2+y2b2=1（a>0，b>0），焦点到椭圆准线的最短距离为33，离心率为32. （1）求椭圆方程；（2）若A为椭圆的上顶点，点T（0，－2）
评价透视 | 齐次化构造解圆锥曲线中定点定值问题

评价透视 | 齐次化构造解圆锥曲线中定点定值问题

摘要：解析几何作为数学学科的必考重点，值得同学们重视起来！定点问题是高考命题的一个热点，也是高考数学的一个难点，要注意定点定值问题是解析几何解答题的考查重点.此类问题定中有动，动中有定，并且常与轨迹问题、曲线系问题等相结合，深入考查直线的圆，圆锥曲线，直线和圆锥曲线位置关系等相关知识.考查数形结合、分类讨论、化归与转化、函数和方程等数学思想方法.定点、定值和定线问题是解析几何中的热点题型，也是高考
评价透视 | 指向核心素养的高一数学作业优化设计

评价透视 | 指向核心素养的高一数学作业优化设计

摘要：优秀的作业对于学生核心素养的提升有很大的帮助，如何以发展数学核心素养为目标、立足学生已有的认知水平优化作业设计是目前一线数学教师面临的一个挑战.本文中以《普通高中数学课程标准（2017年版2020年修订）》提出的六大核心素养为航向标，以2019年人教A版高中数学必修第一册中“指数函数”一节为例进行作业优化设计. 关键词：核心素养；高中数学;作业优化设计;指数函数项目信息：合肥师范学院研
解题天地 | 常规通法中寻求思路，运算变形中寻求突破

解题天地 | 常规通法中寻求思路，运算变形中寻求突破

摘要：2023年新高考Ⅱ卷第21题以双曲线为载体，重点考查学生的转化能力与运算能力，本文中从解题思路分析、解答过程、试题溯源和推广三个方面进行探讨，注重从常规通法中寻求思路，在运算变形中寻求突破. 关键词：圆锥曲线；解题思路；通性通法 1 题目（2023年新高考Ⅱ卷第21题）已知双曲线C的中心为坐标原点，左焦点为（-25，0），离心率为5. （1）求C的方程；（2）记C的左、右顶
解题天地 | 2024年高考数学新课标Ⅰ卷第15题多解探索及教学思考

解题天地 | 2024年高考数学新课标Ⅰ卷第15题多解探索及教学思考

摘要：解三角形问题作为高中数学中的重要内容，不仅考查学生的基础知识掌握情况，还考验其运算求解能力、逻辑推理能力和创新思维.本文中基于2024年高考新课标Ⅰ卷第15题，深入分析该题目的多种解法，探讨如何在教学过程中有效提升学生的解三角形能力，并提出了相应的教学策略. 关键词：高考数学；一题多解；解三角形问题解三角形问题广泛出现在中学数学教材中，尤其是三角函数、正弦定理和余弦定理等章节.这类问题
解题天地 | 开拓数学视角，发散数学思维

解题天地 | 开拓数学视角，发散数学思维

摘要：涉及函数或方程场景中的双变量代数式的最值（或取值范围）问题，以简捷优美的形式设置，巧妙联系“等”与“不等”之间的辩证关系，成为高考、竞赛及强基等数学命题中比较常见的一类基本考查类型.借助一道模拟题中三角方程场景下双变量代数式的最值确定，合理剖析与挖掘，从不同思维视角切入，发散数学思维，进行一题多解，并加以巧妙变式，对学生关键能力的提升与核心素养的养成都有益. 关键词：方程；代数式；最值；函
解题天地 | 追根溯源回归，教学建议引领

解题天地 | 追根溯源回归，教学建议引领

摘要：平面解析几何中轨迹方程的求解问题，是平面解析几何模块中的一个基础知识点，也是新高考中的一个基本考点.结合一道高考真题中有关轨迹方程的确定，合理挖掘问题场景与追根溯源，进而从不同数学思维视角切入，探究轨迹方程求解的技巧与方法，合理总结与归纳，指导数学教学与学习. 关键词：曲线；动点；轨迹；特殊值；数形结合在“三新”（新教材、新课程、新高考）背景下，进一步落实“双减”政策与新改革理念，积极
解题天地 | 两曲线上动点距离的最值问题

解题天地 | 两曲线上动点距离的最值问题

摘要：两条曲线上动点距离的最值问题，分为两类题型，题型一涉及直线上的动点与曲线上的动点的距离，题型二涉及曲线上的动点与另一曲线上的动点的距离.前者主要是把点与点的距离转为为点到直线的距离，后者主要是把点与点的距离最值问题转化为求函数的最值. 关键词：直线；曲线；点与点的距离；最值问题距离问题是高中数学解析几何模块的重要内容.点与点的距离是最基本的问题，进一步，动点与动点距离的最值问题，则是有
解题天地 | 一道抽象函数与其导数交汇问题的多解探究

解题天地 | 一道抽象函数与其导数交汇问题的多解探究

高考与模考试题中，频频出现抽象函数与其导函数的交汇问题，因此，关注此类问题的解法尤为重要.本文中采撷一道模考真题，通过多解探究，旨在拓宽解题思维方法，提升对有关变形技巧和常见规律性结论的灵活运用能力，进一步提高分析、解决此类抽象函数问题的能力. 1 好题采撷（2023年湖北二模第8题）已知函数f（x）及其导函数f′（x）定义域均为R，满足f32+x－f32－x=2x，记g（x）=f′（x），
解题天地 | 一道立体几何考题的多解探究

解题天地 | 一道立体几何考题的多解探究

三棱锥外接球问题是立体几何中的难点，也是高考命题的热点，考查学生的数形结合、函数与方程，以及转化与化归思想等.基于此，本文中拟结合2019年全国卷Ⅰ理科第12题，探讨处理三棱锥外接球问题的常用方法，旨在帮助学生拓宽解题思维视野，提高空间想象能力、数形结合能力，提升数学核心素养. 1 考题再现已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分
解题天地 | 恒等变形巧同构，不等性质妙放缩

解题天地 | 恒等变形巧同构，不等性质妙放缩

摘要：同构思维是解决数学综合问题中一种比较特殊的解题思维与技巧方法.本文中结合一道含参函数的最值问题，借助不等式恒成立的构建，以及关系式的恒等变形，依托同构思维与不等性质的应用，立足同构思维与不等性质求参数的值，归纳总结同构思维与切线不等式思维的解题技巧与规则，合理变式拓展，指导数学教学与复习备考. 关键词：函数；最值；同构；切线不等式；恒成立近几年新高考数学试题中的主观题与客观题，经常出现
解题天地 | 合理代换，巧妙放缩

解题天地 | 合理代换，巧妙放缩

摘要：涉及多变量最值问题，应用场景众多，问题难度较大，掌握一些基本的解题技巧与应对策略是解题的关键所在.结合实例应用，就多变量最值问题解决时的几类常见应对策略加以剖析，总结归纳解题的技巧方法与基本策略，从而指导师生的数学教学与学习及解题研究. 关键词：多变量；最值；消元；基本不等式；代换含有多变量（往往是指双变量及多于两个的变量）的代数式最值（或取值范围）问题，是不等式模块中比较常见的一类题
解题天地 | 代数与三角比翼，推理与运算齐飞

解题天地 | 代数与三角比翼，推理与运算齐飞

摘要：复数作为高考数学命题中的一个基本考点，往往难度较小.而以多选题形式设置的复数综合应用问题，难度有所提升，对于考生“双基”的要求更高.结合一道复数模拟题，就代数思维与三角思维的应用加以分析，强化逻辑推理与数学运算能力，指导数学教学与复习备考. 关键词：复数；代数；三角；模；性质涉及复数的基本运算与基本性质问题，是复数模块考查的一个基本点，也是高考命题的一个基本方向.特别是近年新高考数学试
解题天地 | 乱花渐欲迷人眼，合理消参看本质

解题天地 | 乱花渐欲迷人眼，合理消参看本质

摘要：涉及多变量（三个及以上）代数式的最值（或取值范围）问题，是在双变量基础上的深入与拓展，知识水平与思维能力方面的要求更高.结合一道四变量代数式最值题的探究，合理进行消参转化，透视问题本质，合理归纳总结，巧妙变式拓展，引领并指导数学教学与解题研究. 关键词：变量；代数式；最值；消参；基本不等式含有多变量（这里指三个及其以上数目的变量）的代数式最值（或取值范围）问题，是不等式模块中比较特殊的
解题天地 | 2024年高考数学新高考Ⅱ卷第16题的解法探究

解题天地 | 2024年高考数学新高考Ⅱ卷第16题的解法探究

摘要：涉及函数与导数的综合应用问题，是高考数学试卷中解答题的一种重要考试方向.结合一道高考真题的分析，依托导数的几何意义、函数的极值等设置与应用，从不同思维视角来剖析函数与导数的应用，归纳总结解题规律与技巧策略，合理指导数学复习备考. 关键词：高考；函数；导数；切线；极值高考中有关函数与导数的综合应用问题，是高考数学试卷中的一大基本考点与热点，难度变化较大，场景创设多变，问题设置形式新颖.此
解题天地 | 发散思维应用，巧妙视角变式

解题天地 | 发散思维应用，巧妙视角变式

摘要：解三角形情境下的综合应用问题，可以较好地融合相应的基础知识与基本技能，成为高考命题中的一类常见考查方式.结合一道模拟题，基于解三角形问题的创设及其应用，从不同思维视角切入，合理发散思维，巧妙变式应用，有效指导复习备考. 关键词：三角形；三角函数；最值；基本不等式；辅助角涉及解三角形情境下的综合应用问题，是历年高考中一个基本的考点，场景变化多端，考查形式多样，成为高考中对数学素养的考查要
解题天地 | 例析三角函数最值问题的常见解法及解题技巧

解题天地 | 例析三角函数最值问题的常见解法及解题技巧

三角函数的最值问题是高中数学中的重要内容.在解决这类问题时，有多种有效的方法可供选择.掌握这些方法不仅有助于准确求解三角函数的最值，还能加深对三角函数性质以及相关数学概念之间联系的理解.求解三角函数最值问题的方法有很多，包括基于函数图象、辅助角公式、单调性分析、参数变换和巧用三角函数等方法，在实际解题过程中，应根据具体问题的特点选择合适的方法，灵活运用各种技巧，以提高解题的准确性和效率.同时，通过
教师发展 | 谈高三一轮数学核心概念的有效复习

教师发展 | 谈高三一轮数学核心概念的有效复习

摘要：高三一轮对数学核心概念的复习不应是概念定义的简单再次罗列，然后做题讲题再作业，而应该是启迪与改变学生（特别是中等以下的学生）靠单纯记忆、简单模仿的学习方式，让学生厘清核心概念的形成过程（知其所以然），初步建立系统的知识体系，在核心概念复习过程中掌握必要的数学思想方法，发展概念应用和迁移能力. 关键词：核心概念;一轮复习高三大一轮复习时，相信许多老师在课堂教学中都是生怕知识点的复习做不到
教师发展 | Cosnit-Turtoiu不等式的加强与其他

教师发展 | Cosnit-Turtoiu不等式的加强与其他

设△ABC的三边长分别为a，b，c；外接圆半径、内切圆半径、半周长分别为R，r，s；三条高线分别为ha，hb，hc；面积为Δ.用∑表示循环求和，如∑a=a+b+c. 文［1］介绍了两个不等式：（1）Bokov不等式：在△ABC中，有∑haha-2r≥9. （2）Cosnit-Turtoiu不等式：在△ABC中，有∑ha+rha-r≥6. 本文中对这两个不等式进行一些探讨. 1 Boko

山重水复探试题奥秘柳暗花明显创新思维
一石激起千层浪吹尽黄沙始见金
基于教材的拓展课：一道例题的引申及应用
在例习题教学中提升学生思维品质
多元融合提升高中数学教学质量的策略探究
新课程背景下基于数学史的数学文化在高中数学课堂的应用研究
“阅读与思考”：依托数学文化，学习画法几何
以问题为驱动聚焦核心素养下课堂“真学习”探究
U型探究思维下双曲线单元教学设计
从“一题多解”到“一题多变”
基于数学核心素养的高中数学大单元教学设计的研究
项目式教学的设计与实施
核心素养导向的高中数学大单元教学策略研究
突出概念性质，指向核心素养
基于大单元复习课的项目化学习的教学实践
例谈五环节模式在高中数学教学中的实践
内容自然学得自然教得自然
基于多元表征理论的高中数学教学案例分析
关于“椭圆的几何性质”研究课教学设计的再思考
深度学习铸就活力课堂
借空间动态问题培养直观想象能力
剖析试题情境培养理性思维
设置挑战性学习任务，助推数学思维进阶
转化与化归思想在高中数学试题中的应用特征分析及教学启示
圆锥曲线中几种简化运算的处理方法
巧用“角”，解决双曲线离心率的问题
导数在解三角函数问题中的运用
基于保持特殊性质，探寻动点轨迹
追根溯源链接高考，开拓思维一题多解
巧借积化和差公式，妙破解三角形问题
一道数量积取值范围题的探究
“双新”背景下高中数学分层作业设计及评价研究
着眼高考热点问题聚焦教材难点融合
基于数学问题情境命制的一道概率题目
巧借韦达定理破解斜率之商
齐次化构造解圆锥曲线中定点定值问题
指向核心素养的高一数学作业优化设计
常规通法中寻求思路，运算变形中寻求突破
2024年高考数学新课标Ⅰ卷第15题多解探索及教学思考
开拓数学视角，发散数学思维
追根溯源回归，教学建议引领
两曲线上动点距离的最值问题
一道抽象函数与其导数交汇问题的多解探究
一道立体几何考题的多解探究
恒等变形巧同构，不等性质妙放缩
合理代换，巧妙放缩
代数与三角比翼，推理与运算齐飞
乱花渐欲迷人眼，合理消参看本质
2024年高考数学新高考Ⅱ卷第16题的解法探究
发散思维应用，巧妙视角变式
例析三角函数最值问题的常见解法及解题技巧
谈高三一轮数学核心概念的有效复习
Cosnit-Turtoiu不等式的加强与其他

过往期刊

更多

中学数学·高中版
2025年04期
中学数学·高中版
2025年03期
中学数学·高中版
2025年02期
中学数学·高中版
2025年01期

猜你喜欢

兴趣阅读·少年诗刊
2025年04期
学习方法报·读写拍档新高考版
2025年50期
学习方法报·读写拍档高中版
2025年50期
学习方法报·政治新高考版新教材
2025年48期
学习方法报·历史新教材高一
2025年48期
学习方法报·政治新教材高二
2025年48期
学习方法报·写作（高二）
2025年48期
学习方法报·历史新高考版新教材
2025年48期

Copyright © 2017 龙源数字传媒集团京ICP备060024号
Dragonsource.com Inc. All Rights Reserved
IP:3.137.222.1

上海外国语大学电子阅览室

首页
全部分类
排行榜
客户端下载

登录
个人中心我的收藏退出登录
简体 / 繁体

上海外国语大学电子阅览室

忘记密码新用户

新用户注册

已有账户

注册成功

修改电子邮件